
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是角A,B,C的对边,且
分别是角A,B,C的对边,且![]() .
.
(1)求角![]() 的值;
的值;
(2)已知函数![]() ,将
,将![]() 的图像向左平移
的图像向左平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图像,求
的图像,求![]() 的单调增区间.
的单调增区间.
【答案】(1)由正弦定理得(2sinA+sinC)cosB+sinBcosC=0, ……………… 2分
即 2sinAcosB+sinCcosB+cosCsinB=0,
得 2sinAcosB+sin(B+C)=0, ……………… 3分
因为 A+B+C=π,所以 sin(B+C)=sinA,得 2sinAcosB+sinA=0,
因为 sinA≠0,所以 cosB=![]() , ……………… 5分
, ……………… 5分
又B为三角形的内角,所以B=![]() . ……………… 6分
. ……………… 6分
(2)∵ B=![]() , ∴ f(x)=2cos(2x-
, ∴ f(x)=2cos(2x-![]() ), ………………7分
), ………………7分
∴ g(x)=2cos[2(x+![]() )-
)-![]() ]=2cos(2x-
]=2cos(2x-![]() )=2sin2x, ………………9分
)=2sin2x, ………………9分
由2k![]() -
-![]() ≤2x≤2k
≤2x≤2k![]() +
+![]() (k∈Z),得k
(k∈Z),得k![]() -
-![]() ≤x≤k
≤x≤k![]() +
+![]() (k∈Z),
(k∈Z),
故f(x)的单调增区间为[k![]() -
-![]() ,k
,k![]() +
+![]() ](k∈Z)
](k∈Z)
【解析】略


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】已知Sn是等差数列{an}的前n项和,且S6>S7>S5 , 给出下列五个命题:①d<1;②S11>0;③S12<0;④数列{Sn}中的最大项为S11;⑤|a6|>|a7|.其中正确命题有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF= ![]() ,给出下列结论:
,给出下列结论:
(1)AC⊥BE;
(2)EF∥平面ABCD;
(3)三棱锥A﹣BEF的体积为定值;
(4)异面直线AE,BF所成的角为定值.
其中错误的结论有( )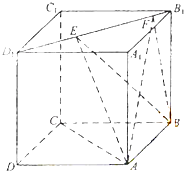
A.0个
B.1 个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正三棱锥P﹣ABC的底面边长为4,侧棱长为8,E,F分别为PB,PC上的动点,求截面△AEF周长的最小值,并求出此时三棱锥P﹣AEF的体积. 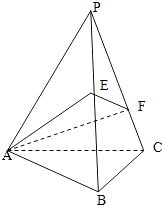
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对应的边分别为a,b,c,sinC+sin(A﹣B)=3sin2B.若 ![]() ,则
,则 ![]() =( )
=( )
A.![]()
B.3
C.![]() 或3
或3
D.3或 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=3,an+1﹣3an=3n(n∈N*),数列{bn}满足bn= ![]() .
.
(Ⅰ)求证:数列{bn}是等差数列,并求数列{an}的通项公式;
(Ⅱ)求数列{an}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知顶点在原点,焦点在x轴上的抛物线被直线y=2x+1截得的弦长为 ![]() .
.
(1)求抛物线的方程;
(2)若抛物线与直线y=2x﹣5无公共点,试在抛物线上求一点,使这点到直线y=2x﹣5的距离最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(
=( ![]() sin
sin ![]() ,1),
,1), ![]() =(cos
=(cos ![]() ,cos2
,cos2 ![]() ).
).
(Ⅰ)若 ![]()
![]() =1,求cos(
=1,求cos( ![]() ﹣x)的值;
﹣x)的值;
(Ⅱ)记f(x)= ![]()
![]() ,在△ABC中,A、B、C的对边分别为a、b、c,且满足(2a﹣c)cosB=bcosC,求函数f(A)的取值范围.
,在△ABC中,A、B、C的对边分别为a、b、c,且满足(2a﹣c)cosB=bcosC,求函数f(A)的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com