
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 当f(x0)≥1时,f[f(x0)]=$lo{g}_{\frac{1}{2}}(f({x}_{0}))$=-2;当f(x0)<1时,f[f(x0)]=1-3f(x0)=-2.由此进行分类讨论,能求出x0的值.
解答 解:∵函数$f(x)=\left\{{\begin{array}{l}{{{log}_{\frac{1}{2}}}x,x≥1}\\{1-3x,x<1}\end{array}}\right.$,f[f(x0)]=-2,
∴①当f(x0)≥1时,f[f(x0)]=$lo{g}_{\frac{1}{2}}(f({x}_{0}))$=-2,
f(x0)=4,则当x0≥1时,f(x0)=$lo{g}_{\frac{1}{2}}{x}_{0}=4$,解得x0=$\frac{1}{16}$,不成立;
当x0<1时,f(x0)=1-3x0=4,解得x0=-1.
②当f(x0)<1时,f[f(x0)]=1-3f(x0)=-2,f(x0)=1.不成立.
综上,x0的值为-1.
故选:A.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
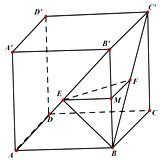 如图,在正方体ABCD-A'B'C'D'中,E,F分别是AB',BC'的中点.
如图,在正方体ABCD-A'B'C'D'中,E,F分别是AB',BC'的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象(如图所示),则f(x)的解析式为$y=2sin(2x+\frac{π}{6})$.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象(如图所示),则f(x)的解析式为$y=2sin(2x+\frac{π}{6})$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数段 | [0~80) | [80~100) | [100~120) | [120~140) | [140~150] |
| 人数 | 300 | 130 | 180 | 220 | 170 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-∞,1]∪[1,+∞) | C. | (-1,0)∪(0,1) | D. | [-1,0)∪(0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
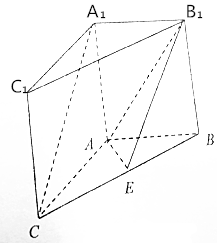 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC,点E是BC上一点,且平面BB1C1C⊥平面AEB1.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC,点E是BC上一点,且平面BB1C1C⊥平面AEB1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com