
分析 由已知及余弦定理可得$\frac{5}{3}$($\frac{a}{b}$)2-2×$\frac{a}{b}$×cosC+$\frac{1}{3}$=0,由于△≥0,可求cosC≥$\frac{\sqrt{5}}{3}$,由于C为锐角,根据正切函数的单调性可求当cosC=$\frac{\sqrt{5}}{3}$时,tanC取最大值,利用同角三角函数基本关系式可求tanC的最大值.
解答 解:∵AB=c=2,AC2-BC2=b2-a2=6,
∴由余弦定理可得:4=a2+b2-2abcosC,
∴$\frac{2}{3}$(b2-a2)=a2+b2-2abcosC,
∴$\frac{5}{3}$($\frac{a}{b}$)2-2×$\frac{a}{b}$×cosC+$\frac{1}{3}$=0,
∵△≥0,
∴可得:cosC≥$\frac{\sqrt{5}}{3}$,
∵b>c,可得C为锐角,
又∵tanC在(0,$\frac{π}{2}$)上单调递增,
∴当cosC=$\frac{\sqrt{5}}{3}$时,tanC取最大值,
∴tanC=$\frac{sinC}{cosC}$=$\frac{\frac{2}{3}}{\frac{\sqrt{5}}{3}}$=$\frac{2\sqrt{5}}{5}$.
故答案为:$\frac{2\sqrt{5}}{5}$.
点评 本题主要考查了余弦定理,正切函数的单调性,同角三角函数基本关系式在解三角形中的应用,考查了方程思想,转化思想,数形结合思想的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
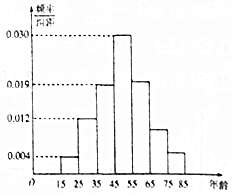 2016年双十一活动结束后,某地区研究人员为了研究该地区在双十一活动中消费超过3000元的人群的年龄状况,随机在当地消费超过3000元的群众中抽取了500人作调查,所得频率分布直方图如图所示:
2016年双十一活动结束后,某地区研究人员为了研究该地区在双十一活动中消费超过3000元的人群的年龄状况,随机在当地消费超过3000元的群众中抽取了500人作调查,所得频率分布直方图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,抛物线y2=4x的一条弦AB经过焦点F,取线段OB的中点D,延长OA至点C,使|OA|=|AC|,过点C,D作y轴的垂线,垂足分别为E,G,则|EG|的最小值为4.
如图,抛物线y2=4x的一条弦AB经过焦点F,取线段OB的中点D,延长OA至点C,使|OA|=|AC|,过点C,D作y轴的垂线,垂足分别为E,G,则|EG|的最小值为4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
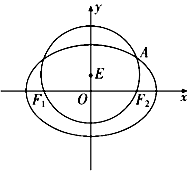 如图,已知圆E:${x^2}+{({y-\frac{1}{2}})^2}=\frac{9}{4}$经过椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.
如图,已知圆E:${x^2}+{({y-\frac{1}{2}})^2}=\frac{9}{4}$经过椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com