
 2016年双十一活动结束后,某地区研究人员为了研究该地区在双十一活动中消费超过3000元的人群的年龄状况,随机在当地消费超过3000元的群众中抽取了500人作调查,所得频率分布直方图如图所示:
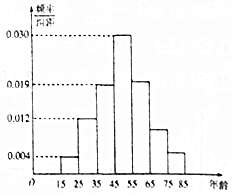
2016年双十一活动结束后,某地区研究人员为了研究该地区在双十一活动中消费超过3000元的人群的年龄状况,随机在当地消费超过3000元的群众中抽取了500人作调查,所得频率分布直方图如图所示:分析 (Ⅰ)由频率分布直方图的性质得(0.004+0.012+0.019+0.030)×10+S1+S2+S3=1,且S1=2S2=4S3.从而得到该地区在双十一活动中消费超过3000元且年龄在[45,65)的频率,由此该地区在双十一活动中消费超过3000元且年龄在[45,65)的人数.
(Ⅱ)年龄在[15,25),[65,75)的频率0.04,0.1,从年龄在[15,25),[65,75)的人群中共抽取7人,年龄在[15,25)的人群中抽取2人,[65,75)的人群抽取5人,再从这7人中随机抽取2人作深入调查,基本事件总数n=${C}_{7}^{2}$=21,至少有1人的年龄在[15,25)内的对立事件是抽取的2人的年龄都在[65,75)内,由此能求出至少有1人的年龄在[15,25)内的概率.
解答 解:(Ⅰ)∵记年龄在[55,65),[65,75),[75,85]对应的小矩形的面积分别是S1,S2,S3,且S1=2S2=4S3.
∴(0.004+0.012+0.019+0.030)×10+S1+S2+S3=1,
且S1=2S2=4S3.
解得S3=0.05,S2=0.1,S3=0.2,
∴该地区在双十一活动中消费超过3000元且年龄在[45,65)的频率为0.030×10+0.2=0.5,
∴该地区在双十一活动中消费超过3000元且年龄在[45,65)的人数为:0.5×30000=15000人.
(Ⅱ)从年龄在[15,25),[65,75)的频率分别为0.004×10=0.04,0.1,
从年龄在[15,25),[65,75)的人群中共抽取7人,
年龄在[15,25)的人群中抽取:7×$\frac{0.04}{0.04+0.1}$=2人,[65,75)的人群抽取:7×$\frac{0.1}{0.04+0.1}$=5人,
再从这7人中随机抽取2人作深入调查,基本事件总数n=${C}_{7}^{2}$=21,
至少有1人的年龄在[15,25)内的对立事件是抽取的2人的年龄都在[65,75)内,
∴至少有1人的年龄在[15,25)内的概率p=1-$\frac{{C}_{5}^{2}}{{C}_{7}^{2}}$=1-$\frac{11}{21}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 非优良 | 优良 | 总计 | |
| 未设立自习室 | 25 | 15 | 40 |
| 设立自习室 | 10 | 30 | 40 |
| 总计 | 35 | 45 | 80 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
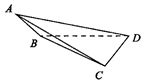 把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在三棱锥A-BCD中,BD⊥CD,AB⊥DB,AC⊥DC,AB=DB=5,CD=4,将围成三棱锥的四个三角形的面积从小到大依次记为S1,S2,S3,S4,设面积为S2的三角形所在的平面为α,则面积为S4的三角形在平面α上的射影的面积是( )
把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在三棱锥A-BCD中,BD⊥CD,AB⊥DB,AC⊥DC,AB=DB=5,CD=4,将围成三棱锥的四个三角形的面积从小到大依次记为S1,S2,S3,S4,设面积为S2的三角形所在的平面为α,则面积为S4的三角形在平面α上的射影的面积是( )| A. | 2$\sqrt{34}$ | B. | $\frac{25}{2}$ | C. | 10 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | 2 | C. | 5 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AB1、BC1的中点.
在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AB1、BC1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com