
(本小题满分12分)已知x∈[- ,
, ],f(x)=tan2x+2tan x+2,求f(x)的最大值和最小值,并求出相应的x值.
],f(x)=tan2x+2tan x+2,求f(x)的最大值和最小值,并求出相应的x值.
当tan x=-1,即x=- 时, y有最小值,ymin=1;当tan x=1,即x=
时, y有最小值,ymin=1;当tan x=1,即x= 时,y有最大值,ymax=5.
时,y有最大值,ymax=5.
解析试题分析:解f(x)=tan2x+2tan x+2=(tan x+1)2+1. ……………2
∵x∈[- ,
, ],∴tan x∈[-
],∴tan x∈[-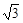 ,1]. ……………6
,1]. ……………6
∴当tan x=-1,即x=- 时, y有最小值,ymin=1;……………9
时, y有最小值,ymin=1;……………9
当tan x=1,即x= 时,y有最大值,ymax=5. ……………12
时,y有最大值,ymax=5. ……………12
考点:二次函数在某闭区间上的最值问题;正切函数的值域。
点评:影响二次函数在闭区间上的最值主要有三个因素:抛物线的开口方向、对称轴和区间的位置。我们常见的并且感到困难的主要是这两类问题:一是动轴定区间,二是定轴动区间。此题是最简单、最基础的二次函数在闭区间上的求最值问题。


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
(本题满分13分)已知函数f(x)=cos(- )+cos(
)+cos( ),k∈Z,x∈R.
),k∈Z,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在[0,π)上的减区间;
(3)若f(α)= ,α∈(0,
,α∈(0, ),求tan(2α+
),求tan(2α+ )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
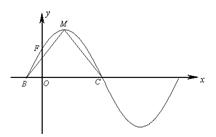
(本小题满分13分)函数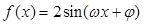
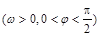 的部分图象如下图所示,该图象与
的部分图象如下图所示,该图象与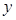 轴交于点
轴交于点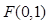 ,与
,与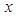 轴交于点
轴交于点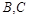 ,
, 为最高点,且
为最高点,且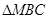 的面积为
的面积为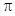 .
.
(Ⅰ)求函数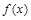 的解析式;
的解析式;
(Ⅱ)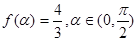 ,求
,求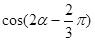 的值.
的值.
(Ⅲ)将函数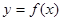 的图象的所有点的横坐标缩短到原来的
的图象的所有点的横坐标缩短到原来的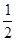 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移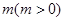 个单位,得函数
个单位,得函数 的图象,若函数
的图象,若函数 为奇函数,求
为奇函数,求 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com