
分析 把极坐标方程转化为直角坐标方程,然后求出极坐标表示的直角坐标,利用点到直线的距离求解即可.
解答 解:直线l的极坐标方程为2ρsin(θ-$\frac{π}{4}$)=$\sqrt{2}$,对应的直角坐标方程为:y-x=1,
点A的极坐标为A(2$\sqrt{2}$,$\frac{7π}{4}$),它的直角坐标为(2,-2).
点A到直线l的距离为:$\frac{|2+2+1|}{\sqrt{2}}$=$\frac{5\sqrt{2}}{2}$.
故答案为:$\frac{5\sqrt{2}}{2}$.
点评 本题考查极坐标与直角坐标方程的互化,点到直线的距离公式的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
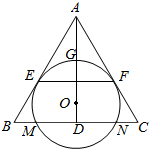 如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.
如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
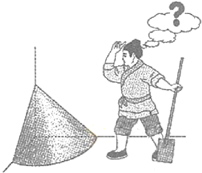 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:”今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?“其意思为:”在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?“已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:”今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?“其意思为:”在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?“已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )| A. | 14斛 | B. | 22斛 | C. | 36斛 | D. | 66斛 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 134石 | B. | 169石 | C. | 338石 | D. | 1365石 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com