
分析 利用双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦距为2$\sqrt{5}$,且双曲线的一条渐近线与直线2x+y=0垂直,求出几何量a,b,c,即可求出双曲线的方程.
解答 解:∵双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦距为2$\sqrt{5}$,∵双曲线的一条渐近线与直线2x+y=0垂直,
∴$\frac{b}{a}$=$\frac{1}{2}$,
∴a=2b,
∵c2=a2+b2,
∴a=2,b=1,
∴双曲线的方程为$\frac{{x}^{2}}{4}-{y}^{2}=1$.
故答案为:$\frac{{x}^{2}}{4}-{y}^{2}=1$.
点评 本题考查双曲线的方程与性质,考查待定系数法的运用,确定双曲线的几何量是关键.


 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 50种 | B. | 49种 | C. | 48种 | D. | 40种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M⊆N | B. | N⊆M | C. | M∩N=∅ | D. | M?N且N?M |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
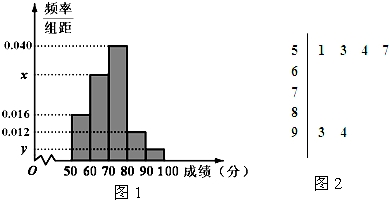
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{{x}^{2}-1}$ | B. | y=ex-e-x | C. | y=ln|x| | D. | y=x${\;}^{\frac{2}{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是一个正三棱柱挖去一个圆柱得到的一个几何体的三视图,则该几何体的体积与挖去的圆柱的体积比为( )
如图是一个正三棱柱挖去一个圆柱得到的一个几何体的三视图,则该几何体的体积与挖去的圆柱的体积比为( )| A. | $\frac{{3\sqrt{3}}}{π}-1$ | B. | $\frac{{3\sqrt{3}}}{π}-\frac{1}{3}$ | C. | $\frac{{3\sqrt{3}}}{π}$ | D. | $\frac{{3\sqrt{3}}}{π}+1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com