练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知Rt△ABC中，∠C=90°．AC=3，BC=4，P为线段AB上的点，且
    CP
    =x•
    CA
    |
    CA
    |
    +y•
    CB
    |
    CB
    |
    ，则xy的最大值为（　　）
    A、1B、2C、3D、4
    考点：平面向量的基本定理及其意义
    专题：平面向量及应用
    分析：想着用一个变量来表示x，y，
    CP
    =
    CA
    +
    AP
    ，
    AP
    和
    AB
    共线，根据共线向量基本定理存在λ使
    AP
    =λ
    AB
    =λ(
    CB
    -
    CA
    )    ，所以
    CP
    =(1-λ)
    CA
    +λ
    CB
    ，所以便得到：
    x
    3
    =1-λ，
    y
    4
    =λ    ，从而解出x，y带入xy即可得到关于λ的函数，求这个函数的最大值即可．
    解答：解：
    CP
    =
    CA
    +
    AP
    =
    CA
    +λ
    AB
    =
    CA
    +λ(
    CB
    -
    CA
    )=(1-λ)
    CA
    +λ
    CB
    （0≤λ≤1）；
    CP
    =
    x
    3
    CA
    +
    y
    4
    CB

    ∴
    1-λ=
    x
    3
    λ=
    y
    4
    ；
    ∴xy=12（1-λ）λ=-12(λ-
    1
    2
    )2+3    ≤3
    当λ=
    1
    2
    时取“=“；
    ∴xy的最大值是3．
    故选C．
    点评：找到一个变量来表示x，y是求解本题的关键，本题考查向量的加法运算，共线向量基本定理，共面向量基本定理，二次函数的最值．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    函数f（x）=1-x+lgx的图象大致是（　　）
    A、
    B、
    C、
    D、

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f（x）=acosax（a∈R）．则下列图象可能为y=f（x）的图象是（　　）
    A、
    B、
    C、
    D、

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某班有男生36人，女生18人，用分层抽样的方法从该班全体学生中抽取一个容量为6的样本，则抽取的女生人数为（　　）
    A、6B、4C、3D、2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某学校用分层抽样的方法从三个年级抽取若干学生，调查“马年春节”学生参加社会实践活动情况，有关数据如下（单位：人）：则x和y的值分别为（　　）
    年级 年级人数 年级人数
    高一 1080 x
    高二 1350 y
    高三 900 20
    A、24，50
    B、24，30
    C、30，24
    D、30，50

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设实系数一元二次方程x2+ax+2b-2=0有两个相异实根，其中一根在区间（0，1）内，另一根在区间（1，2）内，则
    b-4
    a-1
    的取值范围是（　　）
    A、[-
    1
    7
    ，0）
    B、（
    1
    2
    ，
    3
    2
    ）
    C、（-∞，-
    1
    7
    ）
    D、（1，
    3
    2
    ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列关于流程图和结构图的说法中不正确的是（　　）
    A、流程图用来描述一个动态过程
    B、结构图用来刻画系统结构
    C、流程图只能用带箭头的流程线表示各单元的先后关系
    D、结构图只能用带箭头的边线表示各要素之间的从属关系或逻辑上的先后关系

    查看答案和解析>>

    科目：高中数学 来源： 题型：

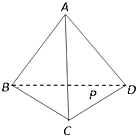    如图，设P为正四面体A-BCD表面（含棱）上与顶点不重合的一点，由点P到四个顶点的距离组成的集合记为M，如果集合M中有且只有2个元素，那么符合条件的点P有（　　）
    A、4个B、6个
    C、10个D、14个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    森林失火了，火正以100m2/min的速度顺风蔓延，消防站接到报警后立即派消防员前去，在失火后5min到达现场开始救火，已知消防队在现场每人每分钟平均可灭火50m2，所消耗的灭火材料、劳务津贴等费用每人每分钟125元，另附加每次救火所损耗的车辆、器械和装备等费用平均每人100元，而每烧毁1m2森林的损失费为60元，设消防队派了x名消防员前去救火，从到达现场开始救火到火全部扑灭共耗时nmin．
    （1）求出x与n的关系式；
    （2）问x为何值时，才能使总损失最小．

    查看答案和解析>>

    同步练习册答案