
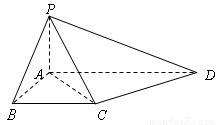
如图,在四棱锥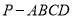 中,底面
中,底面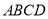 为直角梯形,且
为直角梯形,且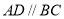 ,
,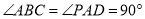 ,侧面
,侧面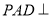 底面
底面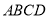 . 若
. 若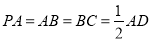 .
.
(1)求证: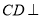 平面
平面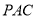 ;
;
(2)侧棱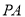 上是否存在点
上是否存在点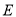 ,使得
,使得 平面
平面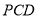 ?若存在,指出点
?若存在,指出点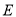 的位置并证明,若不存在,请说明理由;
的位置并证明,若不存在,请说明理由;
(3)求二面角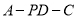 的余弦值.
的余弦值.
(1)见解析(2)见解析(3)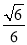
【解析】
试题分析:(1)由侧面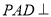 底面
底面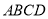 ,PA⊥AD及面面垂直性质定理得,PA⊥面ABCD,由线面垂直定义可得PA⊥CD,通过计算可证CD⊥AC,根据线面垂直判定定理可得CD⊥面PAC;(2)若E是PA中点,F是CD中点,连结BE,EF,CF,由三角形中位线定理及平行公理可证四边形BEFC为平行四边形,则BE∥CF,根据线面平行的判定定理可得;(3)以A为原点,AB,AC,AP分别为
,PA⊥AD及面面垂直性质定理得,PA⊥面ABCD,由线面垂直定义可得PA⊥CD,通过计算可证CD⊥AC,根据线面垂直判定定理可得CD⊥面PAC;(2)若E是PA中点,F是CD中点,连结BE,EF,CF,由三角形中位线定理及平行公理可证四边形BEFC为平行四边形,则BE∥CF,根据线面平行的判定定理可得;(3)以A为原点,AB,AC,AP分别为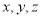 轴建立空间直角坐标系,显然
轴建立空间直角坐标系,显然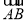 是平面PAD的法向量,求出PCD的法向量,求出这两个法向量的夹角的余弦值,即可求出二面角A-PD—C的余弦值.
是平面PAD的法向量,求出PCD的法向量,求出这两个法向量的夹角的余弦值,即可求出二面角A-PD—C的余弦值.
试题解析:(1)因为 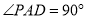 ,所以
,所以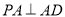 .
.
又因为侧面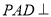 底面
底面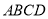 ,且侧面
,且侧面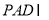 底面
底面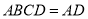 ,
,
所以 底面
底面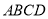 .
.
而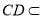 底面
底面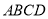 ,
,
所以
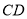 .
.
在底面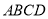 中,因为
中,因为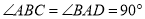 ,
, ,
,
所以 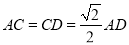 , 所以
, 所以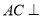
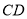 .
.
又因为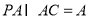 , 所以
, 所以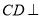 平面
平面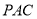 . 4分
. 4分
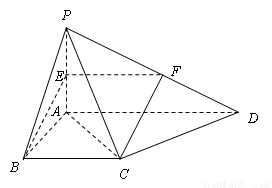
(2)在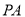 上存在中点
上存在中点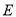 ,使得
,使得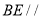 平面
平面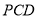 ,
,
证明如下:设 的中点是
的中点是 ,
,
连结 ,
, ,
,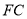 ,
,
则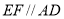 ,且
,且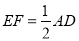 .
.
由已知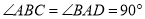 ,
,
所以 . 又
. 又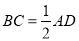 ,
,
所以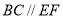 ,且
,且 ,
,
所以四边形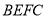 为平行四边形,所以
为平行四边形,所以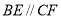 .
.
因为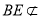 平面
平面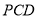 ,
,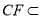 平面
平面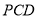 ,
,
所以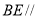 平面
平面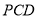 . 8分
. 8分
(3)由(1)知,PA⊥面ABCD,以A为原点,AB,AC,AP分别为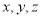 轴建立空间直角坐标系
轴建立空间直角坐标系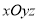 ,设AB=1,则P(0,0,1),B(1,0,0),D(0,2,0),C(1,1,0),则
,设AB=1,则P(0,0,1),B(1,0,0),D(0,2,0),C(1,1,0),则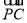 =(1,1,-1),
=(1,1,-1),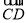 =(-1,1,0),
=(-1,1,0),
显然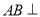 平面
平面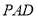 ,所以
,所以
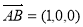 为平面
为平面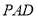 的一个法向量.
的一个法向量.
设面PCD的一个法向量 =(
=(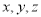 ),则
),则 =
=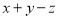 =0且
=0且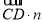 =
= =0,取
=0,取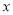 =1,则
=1,则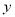 =1,
=1,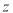 =2,则
=2,则 .
.
设二面角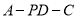 的大小为
的大小为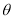 ,由图可知,
,由图可知,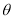 为锐角,
为锐角,
所以
即二面角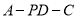 的余弦值为
的余弦值为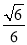 . 12分
. 12分
考点:空间线面垂直、面面垂直判定与性质,空间线面平行的判定与性质,二面角计算


科目:高中数学 来源:2015数学一轮复习迎战高考:1-2命题及其关系、充分条件与必要条件(解析版) 题型:选择题
[2014·荷泽模拟]有以下命题:
①“若xy=1,则x,y互为倒数”的逆命题;
②“面积相等的三角形全等”的否命题;
③“若m≤1,则x2-2x+m=0有实数解”的逆否命题;
④“若A∩B=B,则A⊆B”的逆否命题.
其中真命题为( )
A.①② B.②③ C.④ D.①②③
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
下列式子中不能表示函数y=f(x)的是( ).
A.x=y2+1 B.y=2x2+1
C.x-2y=6 D.x=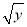
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
已知函数 ,
, ,若有
,若有 ,则b的取值范围为( ).
,则b的取值范围为( ).
A、[2-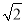 ,2+
,2+ ] B、(2-
] B、(2- ,2+
,2+ )
)
C、[1,3] D、(1,3)
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试理科数学试卷(解析版) 题型:填空题
设函数f(x)=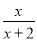 (x>0)
(x>0)
观察:f1(x)=f(x)= ,f2(x)=f(f1(x))=
,f2(x)=f(f1(x))= ,f3(x)=f(f2(x))=
,f3(x)=f(f2(x))= ,
,
f4(x)=f(f3(x))= , 根据以上事实,由归纳推理可得:
, 根据以上事实,由归纳推理可得:
当n∈N*且n≥2时,fn(x)=f(fn-1(x))=________.
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
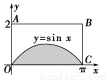
如图,在一个长为π,宽为2的矩形OABC内,曲线y=sin x(0≤x≤π)与x轴围成如图所示的阴影部分,向矩形OABC内随机投一点(该点落在矩形OABC内任何一点是等可能的),则所投的点落在阴影部分的概率是( )
A.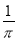 B.
B.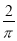 C.
C.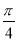 D.
D.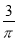
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:填空题
已知边长分别为a、b、c的三角形ABC面积为S,内切圆O半径为r,连接OA、OB、OC,则三角形OAB、OBC、OAC的面积分别为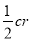 、
、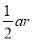 、
、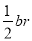 ,由
,由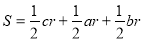 得
得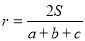 ,类比得四面体的体积为V,四个面的面积分别为
,类比得四面体的体积为V,四个面的面积分别为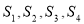 ,则内切球的半径R=_________________
,则内切球的半径R=_________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com