
分析 动点的轨迹是以两定点A(0,$\frac{9}{4}$)、B(0,-$\frac{9}{4}$)为焦点,长轴长为$\frac{41}{2}$的椭圆,由此能求出它的轨迹方程.
解答 解:∵一动点到两定点A(0,$\frac{9}{4}$)、B(0,-$\frac{9}{4}$)的距离之和为$\frac{41}{2}$,
|AB|=$\frac{9}{2}$<$\frac{41}{2}$,
∴动点的轨迹是以两定点A(0,$\frac{9}{4}$)、B(0,-$\frac{9}{4}$)为焦点,长轴长为$\frac{41}{2}$的椭圆,
∴它的轨迹方程为:$\frac{{x}^{2}}{\frac{1681}{16}}$+$\frac{{y}^{2}}{100}$=1.
故答案为:$\frac{{x}^{2}}{\frac{1681}{16}}$+$\frac{{y}^{2}}{100}$=1.
点评 本题考查椭圆的标准方程的求法,是基础题,解题时要认真审题,注意椭圆的定义的合理运用.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:解答题
 有如图所示的五种塑料薄板(厚度不计):
有如图所示的五种塑料薄板(厚度不计):查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
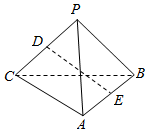 如图,P是平面ABC外一点,PA=4,BC=2$\sqrt{5}$,D,E分别为PC和AB的中点,且DE=3.求异面直线PA和BC所成角的大小.
如图,P是平面ABC外一点,PA=4,BC=2$\sqrt{5}$,D,E分别为PC和AB的中点,且DE=3.求异面直线PA和BC所成角的大小.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
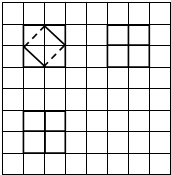 如图所示,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体的体积为( )
如图所示,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体的体积为( )| A. | 6 | B. | $\frac{20}{3}$ | C. | 7 | D. | $\frac{22}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com