
 ����ͼ��ʾ���������ϱ��壨��Ȳ��ƣ���
����ͼ��ʾ���������ϱ��壨��Ȳ��ƣ������� ��1���������֪�ı���PQRS��Ȼ�ǵ������Σ�������QS=PR=QR=4��PQ=PS=RS=x���ֱ����S��Q��QR��RS�Ĵ��ߣ�����ΪI��F�������������ε�������֤���ڢ������ϰ塰�ɲ�������
��2���ֱ���ֱ��������ABCб��BC�ϵĸ�AH������������JKL����JL�ϵĸ�KE������������OMN�ױ��ϵĸ�MG���Ƶ����ڢ٢ڢ��������ϰ塰�ɲ����������ڢۢ��������ϰ塰���ɲ��������ɴ�����������������ϰ�������ȡ����������һ�֡����ɲ������ĸ��ʣ�
��� 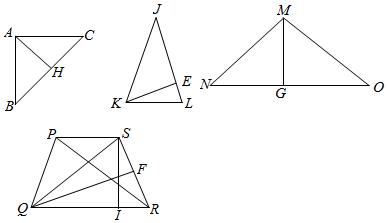 ֤������1���������֪�ı���PQRS��Ȼ�ǵ������Σ�
֤������1���������֪�ı���PQRS��Ȼ�ǵ������Σ�
������QS=PR=QR=4��PQ=PS=RS=x��
�ֱ����S��Q��QR��RS�Ĵ��ߣ�����ΪI��F��
���ɡ�QRF�ס�RSI�õ�$\frac{RI}{RF}=\frac{RS}{QR}$��
��$\frac{{\frac{4-x}{2}}}{{\frac{x}{2}}}=\frac{x}{4}$�����$x=2\sqrt{5}-2$��
��$SI=\sqrt{R{S^2}-I{R^2}}=\sqrt{{x^2}-{{��\frac{4-x}{2}��}^2}}=\sqrt{10-2\sqrt{5}}$��2.4��
��ڢ������ϰ塰�ɲ�������
�⣺��2���ֱ���ֱ��������ABCб��BC�ϵĸ�AH������������JKL����JL�ϵĸ�KE��
����������OMN�ױ��ϵĸ�MG��
����֪��AH=2.4��MG=2.5��
���ɣ�1���ɵõ�������PQRS����ǵ���72�㣬��JKL�ա�PQR����KE=SI��
���ƽ����WXYZ�Ŀ�����$4��\frac{{\sqrt{5}-1}}{2}=2\sqrt{5}-2$��2.4��
��ڢ٢ڢ��������ϰ塰�ɲ����������ڢۢ��������ϰ塰���ɲ�������
������������ϰ�������ȡ����������һ�֡����ɲ������ĸ���$P=\frac{7}{10}$��
���� ���⿼�����ϰ��ܴ���������Ȧ��֤����������ʵ������е��⣬����ʱҪ�������⣬ע���оٷ������������ε����ʵĺ������ã�


 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �ڢ� | C�� | �ڢ� | D�� | �٢� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com