
 中(图1),
中(图1), 是
是 的中点,
的中点, ,
,
 ,
, 将(图1)沿直线
将(图1)沿直线 折起,使二面角
折起,使二面角 为
为 (如图2)
(如图2) 平面
平面 ;
; 与
与 所成角的余弦值;
所成角的余弦值; 到平面
到平面 的距离.
的距离.
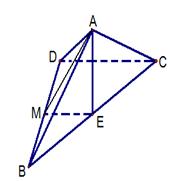 如图取BD中点M,连接AM,ME。因
如图取BD中点M,连接AM,ME。因
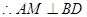 ……1分
……1分 ,
,
 满足:
满足: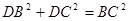 ,
, 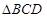 是BC为斜边的直角三角形,
是BC为斜边的直角三角形,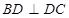 ,
,  是
是 的中点,所以ME为
的中点,所以ME为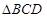 的中位线
的中位线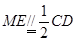 ,
, 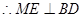 ,
,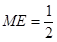 …… 2分
…… 2分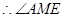 是二面角
是二面角 的平面角
的平面角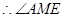 =
= ……3分
……3分 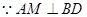 ,
,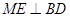 且AM、ME是平面AME内两相交于M的直线
且AM、ME是平面AME内两相交于M的直线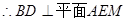
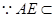 平面AEM
平面AEM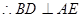 ……4分
……4分 ,
,
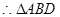 为等腰直角三角形
为等腰直角三角形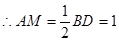 ,
,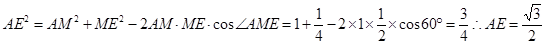
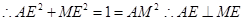 …… 6分
…… 6分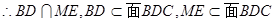
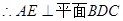 …… 7分
…… 7分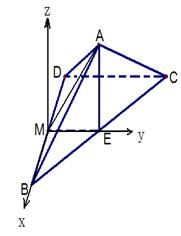 则由(1)及已知条件可知B(1,0,0),
则由(1)及已知条件可知B(1,0,0),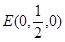 ,
,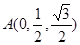 ,D
,D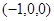 ,C
,C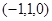
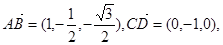 …… 9分
…… 9分 与
与 所成角为
所成角为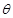 ,
, ……10分
……10分  ……11分
……11分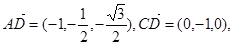 可知
可知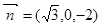 满足,
满足,
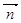 是平面ACD的一个法向量, …… 12分
是平面ACD的一个法向量, …… 12分 到平面
到平面 的距离d,则
的距离d,则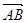 在法向量
在法向量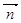 方向上的投影绝对值为d
方向上的投影绝对值为d 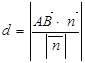 ……13分 所以d
……13分 所以d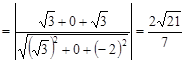 …… 14分
…… 14分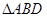 的中位线,MN//AB,又ME//CD
的中位线,MN//AB,又ME//CD 所以直线
所以直线 与
与 所成角为
所成角为 等于MN与ME所成的角,
等于MN与ME所成的角, 或其补角中较小之一 …… 8分
或其补角中较小之一 …… 8分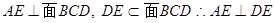 ,N为在
,N为在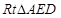 斜边中点
斜边中点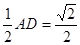 ,MN=
,MN=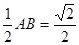 ,ME=
,ME=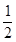 ,
, …….9分
…….9分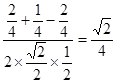 ……10分
……10分 到平面
到平面 的距离d,则三棱锥B-ACD的体积
的距离d,则三棱锥B-ACD的体积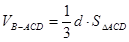 , ……11分
, ……11分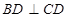
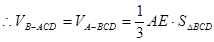 …..12分
…..12分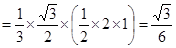
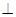 BC
BC 又,
又,
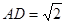 ,
, 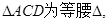
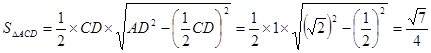 ……13分
……13分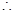
 到平面
到平面 的距离
的距离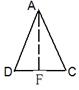
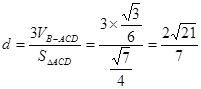 ……14分
……14分  ,
,
 满足:
满足: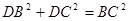 ,
, 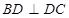 , 1分
, 1分 , A(a,b,c) (由图知a>0,b>0,c>0) …….3分
, A(a,b,c) (由图知a>0,b>0,c>0) …….3分
 ….. 4分
….. 4分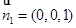 ,
,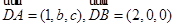 ,所以平面ABD的一个法向量为
,所以平面ABD的一个法向量为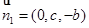 5分
5分 的余弦值
的余弦值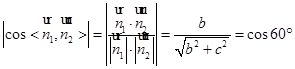 …..6分
…..6分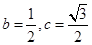 ,
,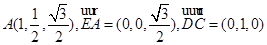 7分
7分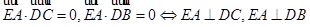 所以
所以 平面
平面 9分
9分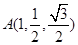 ,D(0,0,0), B(2,0,0),C(0,1,0),
,D(0,0,0), B(2,0,0),C(0,1,0), 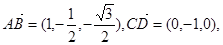
 与
与 所成角为
所成角为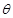 ,则
,则 ……10分
……10分 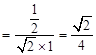 ……11分
……11分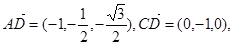 可知
可知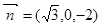 满足,
满足,
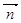 是平面ACD的一个法向量, …… 12分
是平面ACD的一个法向量, …… 12分 到平面
到平面 的距离d,则
的距离d,则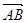 在法向量
在法向量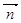 方向上的投影绝对值为d
方向上的投影绝对值为d 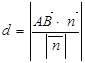 ……13分 所以d
……13分 所以d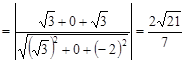 …… 14分
…… 14分

科目:高中数学 来源:不详 题型:解答题
 中,
中,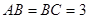 ,
,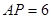 ,
,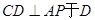 ,现将
,现将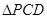 沿线段
沿线段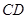 折成
折成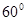 的二面角
的二面角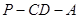 ,设
,设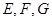 分别是
分别是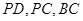 的中点.
的中点.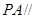 平面
平面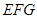 ;
;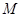 为线段
为线段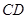 上的动点,问点
上的动点,问点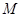 在什么位置时,
在什么位置时,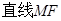 与平面
与平面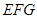 所成角为
所成角为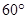 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 的条件是( )
的条件是( )A.平面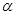 内有无数条直线平行于平面 内有无数条直线平行于平面 |
B.平面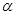 与平面 与平面 同平行于一条直线 同平行于一条直线 |
C.平面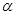 内有两条直线平行于平面 内有两条直线平行于平面 |
D.平面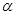 内有两条相交直线平行于平面 内有两条相交直线平行于平面 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com