
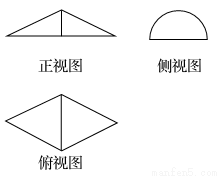
某几何体的三视图如图所示,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:解答题
如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
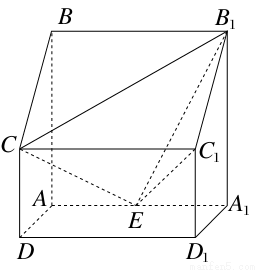
(1)证明:B1C1⊥CE;
(2)求二面角B1-CE-C1的正弦值;
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为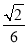 ,求线段AM的长.
,求线段AM的长.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-4直线、平面平行的判定及性质(解析版) 题型:选择题
已知α,β是两个不同的平面,给出下列四个条件:
①存在一条直线a,a⊥α,a⊥β;
②存在一个平面γ,γ⊥α,γ⊥β;
③存在两条平行直线a,b,a?α,b?β,a∥β,b∥α;
④存在两条异面直线a,b,a?α,b?β,a∥β,b∥α.
可以推出α∥β的是( )
A.①③ B.②④ C.①④ D.②③
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-3空间点直线平面之间的位置关系(解析版) 题型:解答题
A是△BCD平面外的一点,E,F分别是BC,AD的中点.
(1)求证:直线EF与BD是异面直线;
(2)若AC⊥BD,AC=BD,求EF与BD所成的角.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-3空间点直线平面之间的位置关系(解析版) 题型:选择题
设A,B,C,D是空间四个不同的点,在下列命题中,不正确的是( )
A.若AC与BD共面,则AD与BC共面
B.若AC与BD是异面直线,则AD与BC是异面直线
C.若AB=AC,DB=DC,则AD=BC
D.若AB=AC,DB=DC,则AD⊥BC
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-2空间几何体的表面积和体积(解析版) 题型:选择题
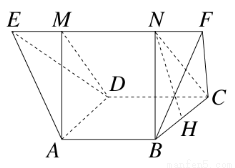
如图,在多面体ABCDEF中,已知四边形ABCD是边长为1的正方形,且△ADE,△BCF均为正三角形,EF∥AB,EF=2,则该多面体的体积为( )
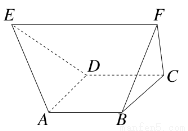
A.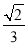 B.
B.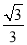 C.
C.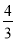 D.
D.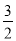
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-2一元二次不等式及其解法(解析版) 题型:填空题
对于满足0≤a≤4的实数a,使x2+ax>4x+a-3恒成立的x取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com