练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设A，B，C，D是空间四个不同的点，在下列命题中，不正确的是(　　)

    A．若AC与BD共面，则AD与BC共面

    B．若AC与BD是异面直线，则AD与BC是异面直线

    C．若AB＝AC，DB＝DC，则AD＝BC

    D．若AB＝AC，DB＝DC，则AD⊥BC

     

    C

    【解析】A中，若AC与BD共面，则A，B，C，D四点共面，则AD与BC共面；B中，若AC与BD是异面直线，则A，B，C，D四点不共面，则AD与BC是异面直线；C中，若AB＝AC，DB＝DC，AD不一定等于BC；D中，若AB＝AC，DB＝DC，可以证明AD⊥BC.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-1直线的倾斜角与斜率、直线方程（解析版） 题型：选择题

    直线ax＋by＋c＝0同时要经过第一、第二、第四象限，则a，b，c应满足(　　)

    A．ab>0，bc<0 B．ab>0，bc>0

    C．ab<0，bc>0 D．ab<0，bc<0

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-5直线、平面垂直的判定及性质（解析版） 题型：选择题

    设m，n是两条不同的直线，α，β，γ是三个不同的平面，有下列四个命题：

    ①若m?β，α⊥β，则m⊥α；②若α∥β，m?α，则m∥β；③若n⊥α，n⊥β，m⊥α，则m⊥β；④若α⊥γ，β⊥γ，m⊥α，则m⊥β.

    其中正确命题的序号是(　　)

    A．①③ B．①② C．③④ D．②③

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-3空间点直线平面之间的位置关系（解析版） 题型：解答题

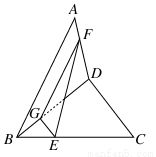
    已知空间四边形ABCD中，AB＝CD＝3，E、F分别是BC、AD上的点，并且BE∶EC＝AF∶FD＝1∶2，EF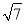＝，求AB和CD所成角的余弦值．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-3空间点直线平面之间的位置关系（解析版） 题型：填空题

    如图所示，在三棱柱ABC－A1B1C1中，AA1⊥底面ABC，AB＝BC＝AA1，∠ABC＝90°，点E、F分别是棱AB、BB1的中点，则直线EF和BC1所成的角是________．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-2空间几何体的表面积和体积（解析版） 题型：填空题

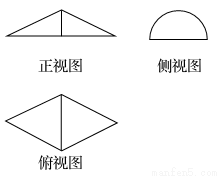
    某几何体的三视图如图所示，其中正视图是腰长为2的等腰三角形，侧视图是半径为1的半圆，则该几何体的表面积是________．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-2空间几何体的表面积和体积（解析版） 题型：选择题

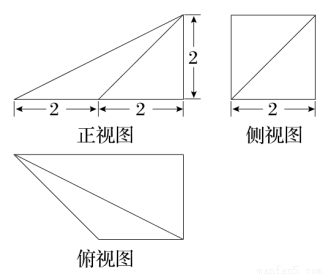
    某几何体的三视图如图所示，则这个几何体的体积为(　　)

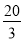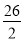    A．4 B． C． D．8

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-7数学归纳法（解析版） 题型：选择题

    用数学归纳法证明1＋2＋3＋…＋(2n＋1)＝(n＋1)(2n＋1)时，从n＝k到n＝k＋1，左边需增添的代数式是(　　)

    A．2k＋2 B．2k＋3

    C．2k＋1 D．(2k＋2)＋(2k＋3)

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-4基本不等式（解析版） 题型：选择题

    设x>0，y>0，且x＋4y＝40，则lgx＋lgy的最大值是(　　)

    A．40 B．10 C．4 D．2

     

    查看答案和解析>>

    同步练习册答案