练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设x>0，y>0，且x＋4y＝40，则lgx＋lgy的最大值是(　　)

    A．40 B．10 C．4 D．2

     

    D

    【解析】∵x＋4y＝40，且x>0，y>0，

    ∴x＋4y≥2＝4.(当且仅当x＝4y时取“＝”)

    ∴4≤40.

    ∴xy≤100.

    ∴lgx＋lgy＝lg(xy)≤lg100＝2.

    ∴lgx＋lgy的最大值为2.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-3空间点直线平面之间的位置关系（解析版） 题型：选择题

    设A，B，C，D是空间四个不同的点，在下列命题中，不正确的是(　　)

    A．若AC与BD共面，则AD与BC共面

    B．若AC与BD是异面直线，则AD与BC是异面直线

    C．若AB＝AC，DB＝DC，则AD＝BC

    D．若AB＝AC，DB＝DC，则AD⊥BC

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-6直接证明与间接证明（解析版） 题型：选择题

    设a，b是两个实数，给出下列条件：

    ①a＋b>1；②a＋b＝2；③a＋b>2；④a2＋b2>2；⑤ab>1.

    其中能推出：“a，b中至少有一个大于1”的条件是(　　)

    A．②③ B．①②③ C．③ D．③④⑤

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-4基本不等式（解析版） 题型：解答题

    某房地产开发公司计划在一楼区内建造一个长方形公园ABCD，公园由形状为长方形A1B1C1D1的休闲区和环公园人行道(阴影部分)组成．已知休闲区A1B1C1D1的面积为4000平方米，人行道的宽分别为4米和10米(如图所示)．

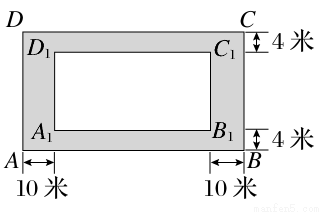
    (1)若设休闲区的长和宽的比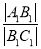＝x(x>1)，求公园ABCD所占面积S关于x的函数S(x)的解析式；

    (2)要使公园所占面积最小，则休闲区A1B1C1D1的长和宽该如何设计？

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-4基本不等式（解析版） 题型：填空题

    若a，b，c>0，且a2＋ab＋ac＋bc＝4，则2a＋b＋c的最小值为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-2一元二次不等式及其解法（解析版） 题型：填空题

    对于满足0≤a≤4的实数a，使x2＋ax>4x＋a－3恒成立的x取值范围是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-2一元二次不等式及其解法（解析版） 题型：填空题

    已知函数f(x)＝，则不等式f(x)－x≤2的解集是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-1不等关系与不等式（解析版） 题型：填空题

    已知－3<b<a<－1，－2<c<－1，则(a－b)c2的取值范围是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：5-3等比数列及其前n项和（解析版） 题型：选择题

    已知正项等比数列{an}满足：a7＝a6＋2a5，若存在两项am，an使得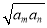＝4a1，则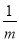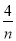＋的最小值为________．

     

    查看答案和解析>>

    同步练习册答案