练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图所示，在三棱柱ABC－A1B1C1中，AA1⊥底面ABC，AB＝BC＝AA1，∠ABC＝90°，点E、F分别是棱AB、BB1的中点，则直线EF和BC1所成的角是________．

     

     

    60°

    【解析】连接AB1，易知AB1∥EF，

    连接B1C交BC1于点G，取AC的中点H，连接GH，则GH∥AB1∥EF.故∠HGB(或其补角)即为EF和BG所成角．设AB＝BC＝AA1＝a，连接HB，在△GHB中，易知GH＝HB＝BG＝a，

    故两直线所成的角即为∠HGB＝60°.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-1直线的倾斜角与斜率、直线方程（解析版） 题型：填空题

    已知点A(3,0)，B(0,4)，直线AB上一动点P(x，y)，则xy的最大值是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-5直线、平面垂直的判定及性质（解析版） 题型：填空题

    设α、β、γ为彼此不重合的三个平面，l为直线，给出下列命题：

    ①若α∥β，α⊥γ，则β⊥γ；

    ②若α⊥γ，β⊥γ，且α∩β＝l，则l⊥γ；

    ③若直线l与平面α内的无数条直线垂直，则直线l与平面α垂直；

    ④若α内存在不共线的三点到β的距离相等，则平面α平行于平面β；

    上面命题中，真命题的序号为________(写出所有真命题的序号)．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-4直线、平面平行的判定及性质（解析版） 题型：选择题

    如图中四个正方体图形，A，B为正方体的两个顶点，M，N，P分别为其所在棱的中点，能得出AB∥平面MNP的图形的序号是(　　)

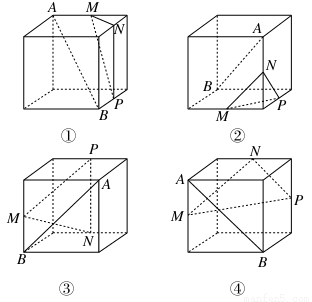
    A．①③ B．①④ C．②③ D．②④

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-3空间点直线平面之间的位置关系（解析版） 题型：选择题

    如图是正方体的展开图，则在这个正方体中：

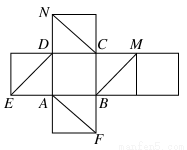
    ①BM与ED平行；

    ②CN与BE是异面直线；

    ③CN与BM成60°角；

    ④DM与BN垂直．

    以上四个命题中，正确命题的序号是(　　)

    A．①②③ B．②④ C．③④ D．②③④

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-3空间点直线平面之间的位置关系（解析版） 题型：选择题

    设A，B，C，D是空间四个不同的点，在下列命题中，不正确的是(　　)

    A．若AC与BD共面，则AD与BC共面

    B．若AC与BD是异面直线，则AD与BC是异面直线

    C．若AB＝AC，DB＝DC，则AD＝BC

    D．若AB＝AC，DB＝DC，则AD⊥BC

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-2空间几何体的表面积和体积（解析版） 题型：解答题

    一个多面体的直观图及三视图如图所示：(其中M、N分别是AF、BC的中点)

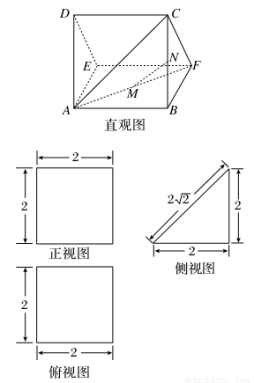
    (1)求证：MN∥平面CDEF；

    (2)求多面体A－CDEF的体积．

     

     

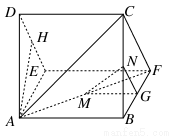
    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-7数学归纳法（解析版） 题型：填空题

    若f(n)＝12＋22＋32＋…＋(2n)2，则f(k＋1)与f(k)的递推关系式是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-4基本不等式（解析版） 题型：填空题

    若a，b，c>0，且a2＋ab＋ac＋bc＝4，则2a＋b＋c的最小值为________．

     

    查看答案和解析>>

    同步练习册答案