
 如图,正方形ABCD的边长为1,E,F分别为BC,CD上异于端点的点,△ECF的周长为2,∠BAE=α,∠DAF=β.
如图,正方形ABCD的边长为1,E,F分别为BC,CD上异于端点的点,△ECF的周长为2,∠BAE=α,∠DAF=β.分析 (Ⅰ)根据解直角三角形,和两角和正弦公式,即可求出,
(Ⅱ)根据解三角形和三角形的周长公式,能求出a+β=$\frac{π}{4}$,再根据向量的数量积,以及三角函数的性质即可求出
解答 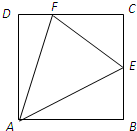 解:(Ⅰ)∵E为BC中点,
解:(Ⅰ)∵E为BC中点,
∴CE=$\frac{1}{2}$,
在Rt△ECF中,设CF=t,
则 EF=$\sqrt{{t}^{2}+(\frac{1}{2})^{2}}$,
∵△ECF的周长为2,
∴$\frac{1}{2}$+t+=$\sqrt{{t}^{2}+(\frac{1}{2})^{2}}$=2,
解得t=$\frac{2}{3}$,即CF=$\frac{2}{3}$;
在Rt△ABE中,AB=1,BE=$\frac{1}{2}$,∠BAE=α,
∴tanα=$\frac{1}{2}$,
在Rt△ADF中,AD=1,DF=$\frac{1}{3}$,∠DAF=β,
∴tanβ=$\frac{1}{3}$,…(2分)
∴tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=1 …(3分)
(Ⅱ)在Rt△ABE中,AB=1,∠BAE=α,
∴BE=tanα∈(0,1),AE=$\frac{1}{cosα}$,
在Rt△ADF中,AD=1,∠DAF=β,
∴DF=tanβ∈(0,1),AF=$\frac{1}{cosβ}$ …(4分)
∴在Rt△ECF中,CE=1-tanα,CF=1-tanβ,
∴EF=$\sqrt{(1-tanα)^{2}+(1-tanβ)^{2}}$,
∵△ECF的周长为2,
∴1-tanα+1-tanβ+$\sqrt{(1-tanα)^{2}+(1-tanβ)^{2}}$=2…(5分)
化简得 tanα+tanβ=1-tanαtanβ,
∴tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=1 …(6分)
又∵0<α+β<$\frac{π}{2}$,
∴a+β=$\frac{π}{4}$,…(7分)
∴∠EAF=$\frac{π}{2}$-(α+β)=$\frac{π}{4}$
∴$\overrightarrow{AE}$•$\overrightarrow{AF}$=|$\overrightarrow{AE}$|•|$\overrightarrow{AF}$|•cos∠EAF=$\frac{1}{cosα}$•$\frac{1}{cosβ}$•cos$\frac{π}{4}$ …(8分)
=$\frac{\sqrt{2}}{2cosαcos(\frac{π}{4}-α)}$=$\frac{2}{\sqrt{2}sin(2α+\frac{π}{4})+1}$ …(10分)
∵0<α<$\frac{π}{4}$,
∴$\frac{π}{4}$<2α+$\frac{π}{4}$<$\frac{3π}{4}$,…(11分)
∴当 2α+$\frac{π}{4}$=$\frac{π}{2}$,即a=$\frac{π}{8}$时,sin(2α+$\frac{π}{4}$)取得最大值1,
即$\overrightarrow{AE}•\overrightarrow{AF}$取得最小值$\frac{2}{\sqrt{2}+1}$=2($\sqrt{2}$-1).…(12分)
点评 本题考查了解三角形的有关问题,以及三角函数的化简,以及向量的数量积公式和正弦函数的性质,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | [-3,1] | C. | (-3,1) | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{3}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com