
分析 由已知中一班有70名同学,而女生30名,二班有50名同学,而女生20名,求出代入条件概型概率公式,可得答案.
解答 解:∵一班和二班两班共有学生120名,
一班有70名同学,而女生30名,
∴二班有50名同学,而女生20名,
∴碰到二班同学的概率为:$\frac{50}{120}$=$\frac{5}{12}$,
而碰到的同学是二班女同学的概率为:$\frac{20}{120}$=$\frac{1}{6}$,
故在碰到二班同学时正好碰到一名女同学的概率为:$\frac{1}{6}$÷$\frac{5}{12}$=$\frac{2}{5}$
点评 本题考查的知识点是古典概型概率计算公式,条件概率,难度不大,属于基础题.


科目:高中数学 来源: 题型:选择题
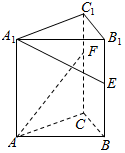 如图,在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6,若E,F分别是棱BB1,CC1上的点,且BE=B1E,C1F=$\frac{1}{3}$CC1,则异面直线A1E与AF所成角的余弦值为( )
如图,在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6,若E,F分别是棱BB1,CC1上的点,且BE=B1E,C1F=$\frac{1}{3}$CC1,则异面直线A1E与AF所成角的余弦值为( )| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{2}}{6}$ | C. | $\frac{\sqrt{3}}{10}$ | D. | $\frac{\sqrt{2}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“p且q”为真 | B. | 命题“p或¬q”为假 | C. | 命题“¬p且q”为真 | D. | 命题“p或q”为假 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?θ∈R,函数f(x)=-2cos(3x+θ)是奇函数 | |
| B. | “?x∈R,x2+1≥0”的否定是“?x0∈R,x02+1<0” | |
| C. | 数列{(n+2)($\frac{9}{10}$)n}的最大项是第7项 | |
| D. | “-1<x<0”是“x<0”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com