Question

7．已知幂函数y=f（x）的图象经过点（3，9），对于偶函数y=g（x）（x∈R），当x≥0时．g（x）=f（x）-2x．
（1）求函数y=f（x）的解析式；
（2）求当x＜0时，函数y=g（x）的解析式，并在给定坐标系下，画出函数y=g（x）的图象；
（3）写出函数y=|g（x）|的单调递减区间．

Answer 1

分析 （1）∵幂函数y=x^α，代入点的坐标可得3^α=9，解方程可得；
（2）当x＜0时，-x＞0，由题意可得g（-x）=x²+2x，再由偶函数可得解析式，可作出图象；
（3）由对称性结合（2）的图象可得函数y=|g（x）|的图象，数形结合可得单调区间．

解答 解：（1）∵幂函数y=f（x）=x^α的图象经过点（3，9），
∴3^α=9，解得α=2，
∴函数y=f（x）的解析式为f（x）=x²；
（2）∵偶函数y=g（x）（x∈R），
当x≥0时，g（x）=x²-2x，
∴当x＜0时，-x＞0，则g（-x）=x²+2x，
由函数为偶函数可得当x＜0时，
g（x）=g（-x）=x²+2x，
函数y=g（x）的图象如图所示；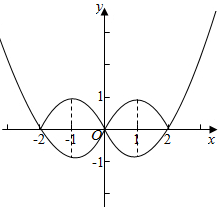

（3）只需将（2）的图象x轴上方的不动，x轴下方的作关于x轴的对称，
可得函数y=|g（x）|的图象（图中红色为对称后的图象），
结合图象可得函数y=|g（x）|的单调递减区间为（-∞，-2）和（-1，0）和（1，2）

点评 本题考查函数的解析式求解的常用方法，涉及函数奇偶性和图象的对称性，属中档题．