
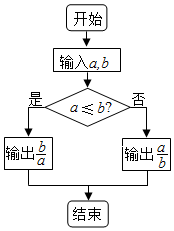
分析 先分别求出 log2$\frac{1}{8}$与($\frac{1}{3}$)-2的值,然后比较大小,选择下一步执行的语句,代入计算即可得解.
解答 解:∵log2$\frac{1}{8}$=-3,($\frac{1}{3}$)-2=9,
∴-3<9,
∴执行输出$\frac{b}{a}$,
∴则(log2$\frac{1}{8}$)?($\frac{1}{3}$)-2=$\frac{9}{-3}$=-3.
故答案为:-3.
点评 本题主要考查了条件结构,含有一个判断框,算法执行到此判断给定的条件P是否成立,选择不同的执行框(A框、B框).无论P条件是否成立,只能执行A框或B框之一,不可能既执行A框又执行B框,也不可能A框、B框都不执行.A框或B框中可以有一个是空的,即不执行任何操作.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{4}$ | B. | $\frac{4}{7}$ | C. | $\frac{7}{8}$ | D. | $\frac{8}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{2}{3}$$\sqrt{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 第一周 | 第二周 | 第三周 | 第四周 | 第五周 | |
| A型数量(台) | 11 | 10 | 15 | A4 | A5 |
| B型数量(台) | 10 | 12 | 13 | B4 | B5 |
| C型数量(台) | 15 | 8 | 12 | C4 | C5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
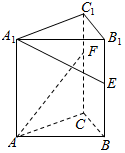 如图,在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6,若E,F分别是棱BB1,CC1上的点,且BE=B1E,C1F=$\frac{1}{3}$CC1,则异面直线A1E与AF所成角的余弦值为( )
如图,在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6,若E,F分别是棱BB1,CC1上的点,且BE=B1E,C1F=$\frac{1}{3}$CC1,则异面直线A1E与AF所成角的余弦值为( )| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{2}}{6}$ | C. | $\frac{\sqrt{3}}{10}$ | D. | $\frac{\sqrt{2}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com