
已知函数f(x)= x3-x2+ax-a(a∈R).
x3-x2+ax-a(a∈R).
(1)当a=-3时,求函数f(x)的极值.
(2)若函数f(x)的图象与x轴有且只有一个交点,求a的取值范围.
(1) 当x=-1时,函数f(x)取得极大值为f(-1)=-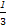 -1+3+3=
-1+3+3=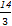 ,
,
当x=3时,函数f(x)取得极小值为f(3)=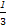 ×27-9-9+3=-6.
×27-9-9+3=-6.
(2) (0,+∞)
【解析】(1)当a=-3时,f(x)=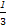 x3-x2-3x+3.
x3-x2-3x+3.
f'(x)=x2-2x-3=(x-3)(x+1).
令f'(x)=0,得x1=-1,x2=3.
当x<-1时,f'(x)>0,
则函数在(-∞,-1)上是增函数,
当-1<x<3时,f'(x)<0,
则函数在(-1,3)上是减函数,
当x>3时,f'(x)>0,
则函数在(3,+∞)上是增函数.
所以当x=-1时,函数f(x)取得极大值为f(-1)=-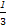 -1+3+3=
-1+3+3=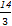 ,
,
当x=3时,函数f(x)取得极小值为f(3)=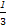 ×27-9-9+3=-6.
×27-9-9+3=-6.
(2)因为f'(x)=x2-2x+a,
所以Δ=4-4a=4(1-a).
①当a≥1时,则Δ≤0,∴f'(x)≥0在R上恒成立,所以f(x)在R上单调递增.
f(0)=-a<0,f(3)=2a>0,所以,当a≥1时函数的图象与x轴有且只有一个交点.
②a<1时,则Δ>0,∴f'(x)=0有两个不等实数根,不妨设为x1,x2(x1<x2),∴x1+x2=2,x1·x2=a,
则
x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
f'(x) | + | 0 | - | 0 | + |
f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
∵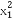 -2x1+a=0,∴a=-
-2x1+a=0,∴a=-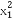 +2x1,
+2x1,
∴f(x1)= -
-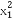 +ax1-a
+ax1-a
= -
-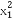 +ax1+
+ax1+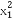 -2x1
-2x1
= +(a-2)x1
+(a-2)x1
=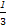 x1[
x1[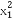 +3(a-2)],
+3(a-2)],
同理f(x2)=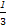 x2[
x2[ +3(a-2)].
+3(a-2)].
∴f(x1)·f(x2)=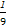 x1x2[
x1x2[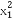 +3(a-2)][
+3(a-2)][ +3(a-2)]=
+3(a-2)]= a(a2-3a+3).
a(a2-3a+3).
令f(x1)·f(x2)>0,解得a>0.
而当0<a<1时,f(0)=-a<0,f(3)=2a>0.
故0<a<1时,函数f(x)的图象与x轴有且只有一个交点.
综上所述,a的取值范围是(0,+∞).


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十 第六章第六节练习卷(解析版) 题型:解答题
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.
(1)sin213°+cos217°-sin 13°cos 17°.
(2)sin215°+cos215°-sin 15°cos 15°.
(3)sin218°+cos212°-sin 18°cos 12°.
(4)sin2(-18°)+cos248°-sin(-18°)cos 48°.
(5)sin2(-25°)+cos255°-sin(-25°)cos 55°.
①试从上述五个式子中选择一个,求出这个常数.
②根据①的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十八第三章第二节练习卷(解析版) 题型:选择题
在△ABC中,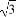 sin(
sin(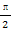 -A)=3sin(π-A),且cosA=-
-A)=3sin(π-A),且cosA=-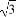 cos(π-B),则C等于( )
cos(π-B),则C等于( )
(A) (B)
(B) (C)
(C)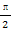 (D)
(D)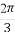
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十五第二章第十二节练习卷(解析版) 题型:填空题
已知f(x)=x3-3x+m在区间[0,2]上任取三个不同的数a,b,c,均存在以f(a),f(b),f(c)为边长的三角形,则m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十五第二章第十二节练习卷(解析版) 题型:选择题
设f(x),g(x)在[a,b]上可导,且f′(x)>g′(x),则当a<x<b时,有( )
(A)f(x)>g(x)
(B)f(x)<g(x)
(C)f(x)+g(a)>g(x)+f(a)
(D)f(x)+g(b)>g(x)+f(b)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十九第三章第三节练习卷(解析版) 题型:填空题
已知直线y=b(b<0)与曲线f(x)=sin(2x+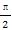 )在y轴右侧依次的前三个交点的横坐标成等比数列,则b的值是 .
)在y轴右侧依次的前三个交点的横坐标成等比数列,则b的值是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十七第三章第一节练习卷(解析版) 题型:选择题
若sinθcosθ>0,则θ在( )
(A)第一、二象限 (B)第一、三象限
(C)第一、四象限 (D)第二、四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com