
分析 (1)利用矩阵可逆的充要条件可知丨A丨≠0,即可求得a的取值范围;
(2)根据矩阵变换的定义,由$[\begin{array}{l}{a}&{1}\\{1}&{a}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$=$[\begin{array}{l}{ax+y}\\{x+ay}\end{array}]$=$[\begin{array}{l}{x′}\\{y′}\end{array}]$,求得x′及y′,代入x'-y'+2a=0,即可求得a的值;
(3)根据矩阵的乘法求得A2,由A4=A2A2,求得A4,A5=A4A,即可求得A5.
解答 解:(1)由矩阵A存在逆矩阵,丨A丨≠0,
∴$|{\begin{array}{l}a&1\\ 1&a\end{array}}|={a^2}-1≠0$,
∴a≠±1…(3分)
(2)设l上任一点为(x,y)在A的作用下变为点(x',y'),
$[\begin{array}{l}{a}&{1}\\{1}&{a}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$=$[\begin{array}{l}{ax+y}\\{x+ay}\end{array}]$=$[\begin{array}{l}{x′}\\{y′}\end{array}]$,
所以$\left\{{\begin{array}{l}{x'=ax+y}\\{y'=x+ay}\end{array}}\right.$…(6分)
所以x'-y'+2a=ax+y-x-ay+2a=(a-1)x+(1-a)y+2a=0,
所以a=2…(9分)
${A^2}=[{\begin{array}{l}2&1\\ 1&2\end{array}}][{\begin{array}{l}2&1\\ 1&2\end{array}}]=[{\begin{array}{l}5&4\\ 4&5\end{array}}]$
(3)${A^4}=[{\begin{array}{l}5&4\\ 4&5\end{array}}][{\begin{array}{l}5&4\\ 4&5\end{array}}]=[{\begin{array}{l}{41}&{40}\\{40}&{41}\end{array}}]$,
${A^5}=[{\begin{array}{l}{41}&{40}\\{40}&{41}\end{array}}][{\begin{array}{l}2&1\\ 1&2\end{array}}]=[{\begin{array}{l}{122}&{121}\\{121}&{122}\end{array}}]$.…(14分)
点评 本题考查矩阵可逆的充要条件,考查矩阵的变换,矩阵的乘法,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
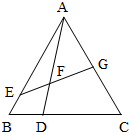 如图,在△ABC中,已知CD=2DB,BA=5BE,AF=mAD,AG=tAC.
如图,在△ABC中,已知CD=2DB,BA=5BE,AF=mAD,AG=tAC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | [0,+∞) | C. | (-∞,0] | D. | [-2,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
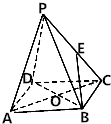 如图,正四棱锥P-ABCD的底面边长为2,侧棱长为$\sqrt{10}$,点O为底面ABCD的中心.
如图,正四棱锥P-ABCD的底面边长为2,侧棱长为$\sqrt{10}$,点O为底面ABCD的中心.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com