
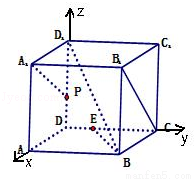
如图,单位正方体ABCD﹣A1B1C1D1中,下列说法错误的是( )
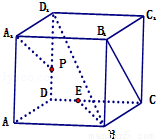
A.BD1⊥B1C
B.若 ,则PE∥A1B
,则PE∥A1B
C.若点B1、A、D、C在球心为O的球面上,则点A、C在该球面上的球面距离为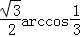
D.若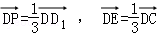 ,则A1P、BE、AD三线共点
,则A1P、BE、AD三线共点
C
【解析】
试题分析:以D点为坐标原点,DA、DC、DD1分别为x、y、z轴建立空间直角坐标系,利用直线所在向量的数量积判定两直线是否垂直,是否平行,利用余弦定理求圆心角,以及利用两平面的公共点肯定在交线上进行判定即可.
【解析】
以D点为坐标原点,DA、DC、DD1分别为x、y、z轴建立空间直角坐标系
则A1(1,0,1),D1(0,0,1),B(1,1,0),B1(1,1,1),C(0,1,0),
选项A: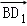 =(﹣1,﹣1,1),
=(﹣1,﹣1,1),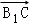 =(﹣1,0,﹣1),则
=(﹣1,0,﹣1),则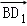 •
•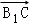 =0∴BD1⊥B1C
=0∴BD1⊥B1C
选项B:若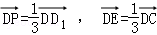 ,则P(0,0,
,则P(0,0, ),E(0,
),E(0, ,0)
,0)
∴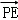 =(0,
=(0, ,﹣
,﹣ ),
),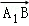 =(0,1,﹣1)则
=(0,1,﹣1)则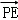 =﹣
=﹣
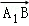 ∴PE∥A1B
∴PE∥A1B
选项C:若点B1、A、D、C在球心为O的球面上,则该球为正方体的外接球,OA=OC=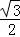 ,AC=
,AC= ;
;
则AC所对的圆心角为π﹣arccos ,∴点A、C在该球面上的球面距离为
,∴点A、C在该球面上的球面距离为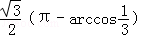 ,则选项C不正确;
,则选项C不正确;
选项D:由选项B可知PE∥A1B,且PE= A1B,∴A1P、BE共面且相交,假设交点为Q,Q∈A1P,A1P?面A1PD,Q∈BE,BE?面BED
A1B,∴A1P、BE共面且相交,假设交点为Q,Q∈A1P,A1P?面A1PD,Q∈BE,BE?面BED
∴Q∈面A1PD,Q∈?面BED,而面A1PD∩面BED=AD∴Q∈AD即A1P、BE、AD三线共点于Q.
故选C.


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源:[同步]2014年湘教版选修2-2 4.2导数的运算练习卷(解析版) 题型:?????
(2014•洛阳二模)已知任何一个三次函数f(x)=ax3+bx2+cx+d(a≠0)都有对称中心M(x0,f(x0)),记函数f(x)的导函数为f′(x),f′(x)的导函数为f″(x),则有f″(x)=0.若函数f(x)=x3﹣3x2,则f( )+f(
)+f(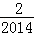 )+f(
)+f( )+…+f(
)+…+f(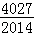 )=( )
)=( )
A.4027 B.﹣4027 C.8054 D.﹣8054
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.9共面与平行练习卷(解析版) 题型:?????
设两不同直线a,b的方向向量分别是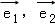 ,平面α的法向量是
,平面α的法向量是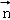 ,
,
则下列推理①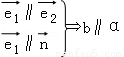 ;②
;②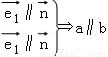 ;③
;③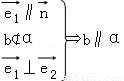 ; ④
; ④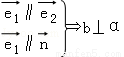 ;
;
其中正确的命题序号是( )
A.①②③ B.②③④ C.①③④ D.①②④
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.9共面与平行练习卷(解析版) 题型:?????
已知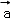 =(1,﹣3,λ),
=(1,﹣3,λ),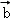 =(2,4,﹣5),若
=(2,4,﹣5),若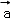 ⊥
⊥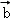 ,则λ=( )
,则λ=( )
A.﹣4 B.﹣2 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.5直线与平面的垂直关系练习卷(解析版) 题型:?????
(2013•绍兴一模)如图,正四面体ABCD的顶点C在平面α内,且直线BC与平面α所成角为45°,顶点B在平面α上的射影为点O,当顶点A与点O的距离最大时,直线CD与平面α所成角的正弦值等于( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.5直线与平面的垂直关系练习卷(解析版) 题型:?????
(2013•山东)已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,体积为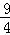 ,底面是边长为
,底面是边长为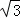 的正三角形,若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )
的正三角形,若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )
A.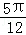 B.
B.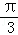 C.
C.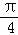 D.
D.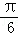
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.1尝试用向量处理空间图形练习卷(解析版) 题型:?????
(理) 在长方体ABCD﹣A1B1C1D1中,以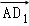 ,
,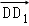 ,
,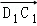 为基底表示
为基底表示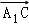 ,其结果是( )
,其结果是( )
A.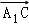 =
=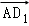 +
+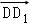 +
+
B.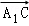 =
=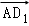
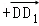

C. =
=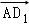 ﹣2
﹣2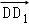 +
+
D.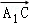 =
=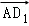
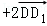
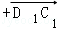
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com