
分析 (1)由题意可表示出长方体的另外的边长,由表面积公式可得;
(2)变形可得S=4x2+$\frac{108}{x}$+$\frac{108}{x}$,由基本不等式可得.
解答 解:(1)由题意可得纸盒底面上较长的边长为2x,
则由体积公式可得72=2x•x•h,(h为纸盒的高),
则h=$\frac{36}{{x}^{2}}$,故S=2•2x•x+2•2x•$\frac{36}{{x}^{2}}$+2•x•$\frac{36}{{x}^{2}}$=4x2+$\frac{216}{x}$,x>0;
(2)∵S=4x2+$\frac{216}{x}$,x>0,∴S=4x2+$\frac{108}{x}$+$\frac{108}{x}$≥3$\root{3}{4{x}^{2}•\frac{108}{x}•\frac{108}{x}}$=108
当且仅当4x2=$\frac{108}{x}$即x=3时取等号.
故当x=3时,做一个这样的长方体纸盒用纸盒最少.
点评 本题考查函数的解析式的求解,涉及基本不等式解决最优化问题,属中档题.


科目:高中数学 来源:2017届湖南石门县一中高三9月月考数学(文)试卷(解析版) 题型:选择题
若函数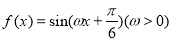 满足
满足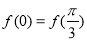 ,且函数在
,且函数在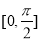 上有且只有一个零点,则
上有且只有一个零点,则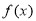 的最小正周期为( )
的最小正周期为( )
A.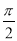 B.
B.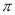 C.
C.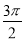 D.
D.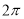
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{x}$)′=$\frac{1}{{x}^{2}}$ | B. | (log2x)′=$\frac{1}{xln2}$ | C. | (3x+1)′=x•3x-1+1 | D. | (cosx)′=sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲正确乙错误 | B. | 甲错误乙正确 | C. | 甲错误乙也错误 | D. | 甲正确乙也正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com