
【题目】已知直线l的方程为![]() x﹣3y+3=0.
x﹣3y+3=0.
(Ⅰ)若直线l1与l在y轴上的截距相等,且l1的倾斜角是l的倾斜角的两倍,求直线l1的一般式方程;
(Ⅱ)若直线l2过点(![]() ,2),且l2与l垂直求直线l2的斜截式方程.
,2),且l2与l垂直求直线l2的斜截式方程.
【答案】(Ⅰ)![]() ;(Ⅱ)y
;(Ⅱ)y![]() x+5.
x+5.
【解析】
(Ⅰ)计算l截距为1,倾斜角为θ![]() ,得到l1的截距和倾斜角得到答案.
,得到l1的截距和倾斜角得到答案.
(Ⅱ)设与直线l垂直的直线方程为:3x![]() y+m=0,代入点坐标,计算得到答案.
y+m=0,代入点坐标,计算得到答案.
(Ⅰ)直线l的方程为![]() x﹣3y+3=0.令x=0,解得y=1,在y轴上的截距为1.
x﹣3y+3=0.令x=0,解得y=1,在y轴上的截距为1.
设l的倾斜角为θ,则tanθ![]() ,θ∈[0,π)∴θ
,θ∈[0,π)∴θ![]() .
.
∵l1的倾斜角是l的倾斜角的两倍,∴l1的倾斜角=2θ![]() .∴tan
.∴tan![]() .
.
∴直线l1的方程为:y![]() x+1即
x+1即![]()
(Ⅱ)设与直线l垂直的直线方程为:3x![]() y+m=0.
y+m=0.
把点(![]() ,2)代入可得:3
,2)代入可得:3![]() 2
2![]() m=0.解得m=﹣5
m=0.解得m=﹣5![]() .
.
∴直线l2过点(![]() ,2),且l2与l垂直的直线方程为:3x
,2),且l2与l垂直的直线方程为:3x![]() y﹣5
y﹣5![]() 0.
0.
化为:![]() x+y﹣5=0,其斜截式方程为:y
x+y﹣5=0,其斜截式方程为:y![]() x+5.
x+5.


科目:高中数学 来源: 题型:
【题目】某中学有初中学生1800人,高中学生1200人.为了解学生本学期课外阅读时间,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们课外阅读时间,然后按“初中学生”和“高中学生”分为两组,再将每组学生的阅读时间(单位:小时)分为5组:[0,10),[10,20),[20,30),[30,40),[40,50],并分别加以统计,得到如下图所示的频率分布直方图.

(I)写出a的值;
(II)试估计该校所有学生中,阅读时间不小于30个小时的学生人数;
(III)从阅读时间不足10个小时的样本学生中随机抽取3人,并用X表示其中初中生的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近![]() 个月广告投入量
个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 |
|
|
|
|
|
|
广告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他们分别用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
|
|
|
|

(Ⅰ)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由;
(Ⅱ)残差绝对值大于![]() 的数据被认为是异常数据,需要剔除:
的数据被认为是异常数据,需要剔除:
(ⅰ)剔除异常数据后求出(Ⅰ)中所选模型的回归方程
(ⅱ)若广告投入量![]() 时,该模型收益的预报值是多少?
时,该模型收益的预报值是多少?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
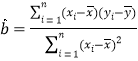
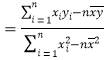 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解本届高二学生对文理科的选择与性别是否有关,现随机从高二的全体学生中抽取了若干名学生,据统计,男生35人,理科生40人,理科男生30人,文科女生15人。
(1)完成如下2×2列联表,判断是否有99.9%的把握认为本届高二学生“对文理科的选择与性别有关”?
男生 | 女生 | 合计 | |
文科 | |||
理科 | |||
合计 |
(2)已采用分层抽样的方式从样本的所有女生中抽取了5人,现从这5人中随机抽取2人参加座谈会,求抽到的2人恰好一文一理的概率。
| 0.15 | 0.10 | 0.05 | 0.01 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(参考公式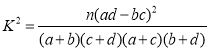 ,其中
,其中![]() 为样本容量)
为样本容量)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
![]() Ⅰ
Ⅰ![]() 当
当![]() 时,
时,![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
![]() Ⅱ
Ⅱ![]() 设
设![]() 是定义在
是定义在![]() 上的函数,在
上的函数,在![]() 内任取
内任取![]() 个数
个数![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() ,令
,令![]() ,
,![]() ,如果存在一个常数
,如果存在一个常数![]() ,使得
,使得![]() 恒成立,则称函数
恒成立,则称函数![]() 在区间
在区间![]() 上的具有性质P.试判断函数
上的具有性质P.试判断函数![]() 在区间
在区间![]() 上是否具有性质P?若具有性质P,请求出M的最小值;若不具有性质P,请说明理由.
上是否具有性质P?若具有性质P,请求出M的最小值;若不具有性质P,请说明理由.![]() 注:
注:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品销售价格和销售量与销售天数有关,第x天![]() 的销售价格
的销售价格![]() (元/百斤),第x天
(元/百斤),第x天![]() 的销售量
的销售量![]() (百斤)(a为常数),且第7天销售该商品的销售收入为2009元.
(百斤)(a为常数),且第7天销售该商品的销售收入为2009元.
(1)求第10天销售该商品的销售收入是多少?
(2)这20天中,哪一天的销售收入最大?为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com