
【题目】某中学有初中学生1800人,高中学生1200人.为了解学生本学期课外阅读时间,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们课外阅读时间,然后按“初中学生”和“高中学生”分为两组,再将每组学生的阅读时间(单位:小时)分为5组:[0,10),[10,20),[20,30),[30,40),[40,50],并分别加以统计,得到如下图所示的频率分布直方图.

(I)写出a的值;
(II)试估计该校所有学生中,阅读时间不小于30个小时的学生人数;
(III)从阅读时间不足10个小时的样本学生中随机抽取3人,并用X表示其中初中生的人数,求X的分布列和数学期望.
【答案】(I).a=0.03.(II).870人.
(III)所以X的分布列为:
X | 1 | 2 | 3 |
P |
|
|
|
E(X)=![]() .
.
【解析】试题分析:(1)根据各矩形面积之和为![]() ,可求得
,可求得![]() 的值;(2)先根据直方图算出初中生中,阅读时间不小于
的值;(2)先根据直方图算出初中生中,阅读时间不小于![]() 个小时的学生频率以及高中生中,阅读时间不小于
个小时的学生频率以及高中生中,阅读时间不小于![]() 个小时的学生频率,结合总人数可估计该校所有学生中,阅读时间不小于
个小时的学生频率,结合总人数可估计该校所有学生中,阅读时间不小于![]() 个小时的学生人数;(3)
个小时的学生人数;(3)![]() 的可能取值
的可能取值![]() ,利用组合知识结合古典概型概率公式求出各随机变量对应的概率,从而可得分布列,进而利用期望公式可得
,利用组合知识结合古典概型概率公式求出各随机变量对应的概率,从而可得分布列,进而利用期望公式可得![]() 的数学期望.
的数学期望.
试题解析:(I).a=0.03.
(II)由分层抽样,知抽取的初中生有60名,高中生有40名.
因为初中生中,阅读时间不小于30个小时的学生频率为(0.02+0.005)×10=0.25,
所以所有的初中生中,阅读时间不小于30个小时的学生约有0.25×1800=450人,
同理,高中生中,阅读时间不小于30个小时的学生频率为(0.03+0.005)×10=0.35,学生人数约有0.35×1200=420人.
所以该校所有学生中,阅读时间不小于30个小时的学生人数约有450+420=870人.
(III).初中生中,阅读时间不足10个小时的学生频率为0.005×10=0.05,样本人数为0.05×60=3人.
同理,高中生中,阅读时间不足10个小时的学生样本人数为(0.005×10)×40=2人.
故X的可能取值为l,2,3.
则P(X=1)=![]() ,P(X=2)=
,P(X=2)=![]() ,P(
,P(![]() .
.
所以X的分布列为:
X | 1 | 2 | 3 |
P |
|
|
|
所以E(X)=1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() .
.


科目:高中数学 来源: 题型:
【题目】某市政府为了节约生活用电,计划在本市试行居民生活用电定额管理,即确定一户居民月用电量标准a,用电量不超过a的部分按平价收费,超出a的部分按议价收费![]() 为此,政府调查了100户居民的月平均用电量
为此,政府调查了100户居民的月平均用电量![]() 单位:度
单位:度![]() ,以
,以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图所示.
分组的频率分布直方图如图所示.
![]() 根据频率分布直方图的数据,求直方图中x的值并估计该市每户居民月平均用电量
根据频率分布直方图的数据,求直方图中x的值并估计该市每户居民月平均用电量![]() 的值;
的值;
![]() 用频率估计概率,利用
用频率估计概率,利用![]() 的结果,假设该市每户居民月平均用电量X服从正态分布
的结果,假设该市每户居民月平均用电量X服从正态分布![]()
![]() 估计该市居民月平均用电量介于
估计该市居民月平均用电量介于![]() 度之间的概率;
度之间的概率;
![]() 利用
利用![]() 的结论,从该市所有居民中随机抽取3户,记月平均用电量介于
的结论,从该市所有居民中随机抽取3户,记月平均用电量介于![]() 度之间的户数为
度之间的户数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某长产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若近几年该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() 满足的函数关系式为
满足的函数关系式为![]() ,且每年该农产品都能售完.
,且每年该农产品都能售完.
①根据(1)中所建立的回归方程预测该地区2018(![]() )年该农产品的产量;
)年该农产品的产量;
②当![]() (
(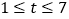 )为何值时,销售额
)为何值时,销售额![]() 最大?
最大?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: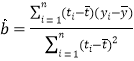 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秸秆还田是当今世界上普通重视的一项培肥地力的增产措施,在杜绝了秸秆焚烧所造成的大气污染的同时还有增肥增产作用.某农机户为了达到在收割的同时让秸秆还田,花![]() 元购买了一台新型联合收割机,每年用于收割可以收入
元购买了一台新型联合收割机,每年用于收割可以收入![]() 万元(已减去所用柴油费);该收割机每年都要定期进行维修保养,第一年由厂方免费维修保养,第二年及以后由该农机户付费维修保养,所付费用
万元(已减去所用柴油费);该收割机每年都要定期进行维修保养,第一年由厂方免费维修保养,第二年及以后由该农机户付费维修保养,所付费用![]() (元)与使用年数
(元)与使用年数![]() 的关系为:
的关系为:![]() ,已知第二年付费
,已知第二年付费![]() 元,第五年付费
元,第五年付费![]() 元.
元.
(1)试求出该农机户用于维修保养的费用![]() (元)与使用年数
(元)与使用年数![]() 的函数关系;
的函数关系;
(2)这台收割机使用多少年,可使平均收益最大?(收益=收入-维修保养费用-购买机械费用)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的方程为![]() x﹣3y+3=0.
x﹣3y+3=0.
(Ⅰ)若直线l1与l在y轴上的截距相等,且l1的倾斜角是l的倾斜角的两倍,求直线l1的一般式方程;
(Ⅱ)若直线l2过点(![]() ,2),且l2与l垂直求直线l2的斜截式方程.
,2),且l2与l垂直求直线l2的斜截式方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com