
分析 设$A=[{\begin{array}{l}a&b\\ c&d\end{array}}]$,根据矩阵变换,列方程组,即可求得a、b、c和d的值,求得A.
解答 解:设$A=[{\begin{array}{l}a&b\\ c&d\end{array}}]$,
因为向量$[\begin{array}{l}\;1\\-1\end{array}]$是矩阵A的属于特征值-1的一个特征向量,
所以$[{\begin{array}{l}a&b\\ c&d\end{array}}][{\begin{array}{l}1\\{-1}\end{array}}]=(-1)[{\begin{array}{l}1\\{-1}\end{array}}]=[{\begin{array}{l}{-1}\\ 1\end{array}}]$.所以$\left\{\begin{array}{l}a-b=-1\\ c-d=1\end{array}\right.$…4分
因为点P(1,1)在矩阵A对应的变换作用下变为P'(3,3),
所以$[{\begin{array}{l}a&b\\ c&d\end{array}}][{\begin{array}{l}1\\ 1\end{array}}]=[{\begin{array}{l}3\\ 3\end{array}}]$.所以$\left\{\begin{array}{l}a+b=3\\ c+d=3\end{array}\right.$…8分
解得a=1,b=2,c=2,d=1,所以$A=[{\begin{array}{l}1&2\\ 2&1\end{array}}]$.…10分.
点评 本题考查矩阵的变换,考查方程思想,体现转化思想,属于中档题.


科目:高中数学 来源: 题型:解答题
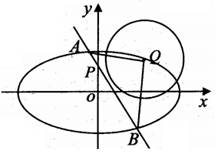 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,圆Q:x2+y2-4x-2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,圆Q:x2+y2-4x-2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
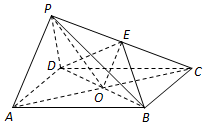 如图,在四棱锥P-ABCD中,四边形ABCD为平行四边形,AC,BD相交于点O,点E为PC的中点,OP=OC,PA⊥PD.求证:
如图,在四棱锥P-ABCD中,四边形ABCD为平行四边形,AC,BD相交于点O,点E为PC的中点,OP=OC,PA⊥PD.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(2)>f(e)>f(3) | B. | f(3)>f(e)>f(2) | C. | f(3)>f(2)>f(e) | D. | f(e)>f(3)>f(2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com