
分析 (1)由f(x)=a-$\frac{2}{x}$,分别求出f(1)和f(2),再由2f(1)=f(2),能求出a.
(2)由(1)得f(x)=3-$\frac{2}{x}$在(-∞,0)上单调递增.利用定义能进行证明.
解答 解:(1)∵f(x)=a-$\frac{2}{x}$,
∴f(1)=a-$\frac{2}{1}$=a-2,f(2)=a-$\frac{2}{2}$=a-1,
∵2f(1)=f(2),2(a-2)=a-1,解得a=3.
(2)由(1)得f(x)=3-$\frac{2}{x}$在(-∞,0)上单调递增.
证明:任取x1,x2∈(-∞,0),且x1<x2,
f(x1)-f(x2)=(3-$\frac{2}{{x}_{1}}$)-(3-$\frac{2}{{x}_{2}}$)=$\frac{2}{{x}_{2}}-\frac{2}{{x}_{1}}$=$\frac{2({x}_{1}-{x}_{2})}{{x}_{1}{x}_{2}}$,
由x1-x2<0,x1<0,x2<0,
得$\frac{2({x}_{1}-{x}_{2})}{{x}_{1}{x}_{2}}<0$,
∴f(x1)<f(x2),
因此f(x)为单调增函数.
点评 本题考查实数值的求法,考查函数的单调性的判断与证明,是基础题,解题时要认真审题,注意函数性质的合理运用.


科目:高中数学 来源: 题型:填空题
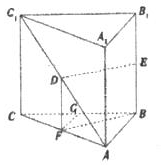 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=$\sqrt{3}$,D、E分别是AC1和BB1的中点,则直线BF与平面BB1C1C所成的角为30°.
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=$\sqrt{3}$,D、E分别是AC1和BB1的中点,则直线BF与平面BB1C1C所成的角为30°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
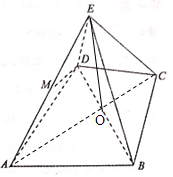 如图几何体E-ABCD是四棱锥,△ABD为正三角形,∠BCD=120°,CB=CD=CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD,
如图几何体E-ABCD是四棱锥,△ABD为正三角形,∠BCD=120°,CB=CD=CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
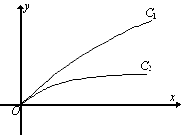 如图,当参数λ=λ1,λ2时,连续函数y=$\frac{x}{1+λx}$(x≥0)的图象分别对应曲线C1和C2,则( )
如图,当参数λ=λ1,λ2时,连续函数y=$\frac{x}{1+λx}$(x≥0)的图象分别对应曲线C1和C2,则( )| A. | 0<λ2<λ1 | B. | λ2<λ1<0 | C. | λ1<λ2<0 | D. | 0<λ1<λ2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com