
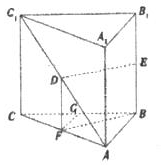
 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=$\sqrt{3}$,D、E分别是AC1和BB1的中点,则直线BF与平面BB1C1C所成的角为30°.
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=$\sqrt{3}$,D、E分别是AC1和BB1的中点,则直线BF与平面BB1C1C所成的角为30°. 分析 取AC的中点为F,连接BF、DF.根据题意得ED∥BF,进而得到直线DE与平面BB1C1C所成的角等于直线BF与平面BB1C1C所成的角,从而可得结论.
解答 解:取AC的中点为F,连接BF、DF.
∵在直三棱柱ABC-A1B1C1中,且D,E分别是AC1和BB1的中点,
∴ED∥BF.
过点F作FG垂直于BC交BC于点G,由题意得∠FBG即为所求的角.
∵AB=1,AC=2,∠ABC=90°,
∴∴∠BCA=30°,
∴在△FBG中∠FBG=30°.
故答案为30°.
点评 本题考查线面角,考查学生的计算能力,解决此类问题的关键是熟悉线面角的作法,即由线上的一点作平面的垂线再连接斜足与垂足则得到线面角.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | 3 | C. | 1 | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-80]∪[-16,+∞) | B. | [-80,-16] | C. | (-∞,16]∪[80,+∞) | D. | [16,80] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | π | C. | -π | D. | 没有正确答案 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,+∞) | B. | [0,+∞) | C. | (-∞,0] | D. | (-∞,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com