
分析 由题意可知:|F1C|=|CO|=$\frac{1}{2}$,由|CM|=|CN|.原点O在以线段MN为直径的圆上,则|OA|=|OB|=c=1.由椭圆的性质,可知$\left\{\begin{array}{l}{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{a}^{2}-1}=1}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,可得到A点坐标,从而求出OA的斜率,由直线AB斜率为0<k≤$\sqrt{3}$,求出a的取值范围,从而求出e的取值范围.
解答 解:由椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点在x轴上,记线段MN与x轴交点为C,
由AF1的中点为M,BF1的中点为N,
∴MN∥AB,|F1C|=|CO|=$\frac{1}{2}$,
∵A、B为椭圆上关于原点对称的两点,
∴|CM|=|CN|.
∵原点O在以线段MN为直径的圆上,
∴|CO|=|CM|=|CN|=$\frac{1}{2}$.
∴|OA|=|OB|=c=1.
∵|OA|>b,
∴a2=b2+c2<2c2,
∴e=$\frac{c}{a}$>$\frac{\sqrt{2}}{2}$.
设A(x,y),
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{a}^{2}-1}=1}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}^{2}={a}^{2}(2-{a}^{2})}\\{{y}^{2}=1-2{a}^{2}+{a}^{4}}\end{array}\right.$.
AB的倾斜角α∈(0,$\frac{π}{3}$),
∴直线AB斜率为0<k≤$\sqrt{3}$,
∴0<$\frac{1-2{a}^{2}+{a}^{4}}{{a}^{2}(2-{a}^{2})}$≤3,
∴1-$\frac{\sqrt{3}}{2}$≤a2≤1+$\frac{\sqrt{3}}{2}$,
即为$\frac{\sqrt{3}-1}{2}$≤a≤$\frac{\sqrt{3}+1}{2}$,
∴e=$\frac{c}{a}$=$\frac{1}{a}$∈[$\sqrt{3}$-1,$\sqrt{3}$+1],
由于0<e<1,
∴离心率e的取值范围为[$\sqrt{3}$-1,1).
故答案为:[$\sqrt{3}$-1,1).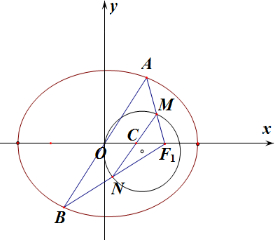
点评 本题考查椭圆的方程和性质,主要考查椭圆方程的运用,同时考查圆的性质和直线斜率公式的运用,考查运算能力,属于难题.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | (-∞,0] | C. | [-$\frac{1}{2}$,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,平面上有四个点A、B、P、Q,其中A、B为定点,且AB=$\sqrt{3}$,P、Q为动点,满足AP=PQ=QB=1,又△APB和△PQB的面积分别为S和T,则S2+T2的最大值为( )
如图,平面上有四个点A、B、P、Q,其中A、B为定点,且AB=$\sqrt{3}$,P、Q为动点,满足AP=PQ=QB=1,又△APB和△PQB的面积分别为S和T,则S2+T2的最大值为( )| A. | $\frac{6}{7}$ | B. | 1 | C. | $\sqrt{3}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
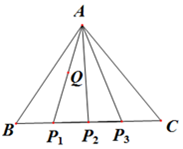 设△ABC是边长为1的正三角形,点P1,P2,P3四等分线段BC(如图所示).
设△ABC是边长为1的正三角形,点P1,P2,P3四等分线段BC(如图所示).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-2=0 | B. | y-1=0 | C. | x-y=0 | D. | x+3y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\sqrt{{x}^{2}}$,g(x)=x | B. | f(x)=x,g(x)=$\frac{{x}^{2}}{x}$ | ||
| C. | f(x)=lnx2,g(x)=2lnx | D. | f(x)=logaax(a>0,a≠1),g(x)=$\root{3}{{x}^{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
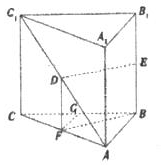 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=$\sqrt{3}$,D、E分别是AC1和BB1的中点,则直线BF与平面BB1C1C所成的角为30°.
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=$\sqrt{3}$,D、E分别是AC1和BB1的中点,则直线BF与平面BB1C1C所成的角为30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com