
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据f(x)为奇函数,可设x>0,从而有-x<0,从而可求出f(x)=e-x(x-1),从而可看出-1,1,0都是f(x)的零点,这便得出①②错误,而由f(x)解析式便可解出f(x)>0的解集,从而判断出③的正误,可分别对x<0和x>0时的f(x)求导数,根据导数符号可判断f(x)的单调性.
解答 解:对于①,f(x)为R上的奇函数,设x>0,-x<0,则:f(-x)=e-x(-x+1)=-f(x);
∴f(x)=e-x(x-1),∴①错误;
对于②,∵f(-1)=0,f(1)=0;又f(0)=0;
∴f(x)有3个零点,∴②错误;
对于③,当x<0时,f(x)=ex(x+1);∴-1<x<0时,f(x)>0;
当x>0时,f(x)=e-x(x-1);∴x>1时,f(x)>0;
∴f(x)>0的解集为(-1,0)∪(1,+∞),∴③正确;
对于④,(1)x<0时,f′(x)=ex(x+2);
∴x<-2时,f′(x)<0,-2<x<0时,f′(x)>0;
∴f(x)在(-∞,-2上单调递减,在(-2,0)上单调递增;
∴④错.
故选:A
点评 考查奇函数的定义,对于奇函数,已知一区间上的解析式,求其对称区间上解析式的方法,函数零点的定义及求法,指数函数的值域,以及根据导数符号判断函数单调性,属于中档题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
 如图,平面上有四个点A、B、P、Q,其中A、B为定点,且AB=$\sqrt{3}$,P、Q为动点,满足AP=PQ=QB=1,又△APB和△PQB的面积分别为S和T,则S2+T2的最大值为( )
如图,平面上有四个点A、B、P、Q,其中A、B为定点,且AB=$\sqrt{3}$,P、Q为动点,满足AP=PQ=QB=1,又△APB和△PQB的面积分别为S和T,则S2+T2的最大值为( )| A. | $\frac{6}{7}$ | B. | 1 | C. | $\sqrt{3}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
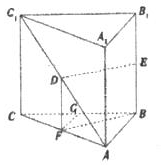 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=$\sqrt{3}$,D、E分别是AC1和BB1的中点,则直线BF与平面BB1C1C所成的角为30°.
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=$\sqrt{3}$,D、E分别是AC1和BB1的中点,则直线BF与平面BB1C1C所成的角为30°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{18}{5}$ | B. | $\frac{14}{5}$ | C. | $\frac{12}{5}$ | D. | $\frac{9}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
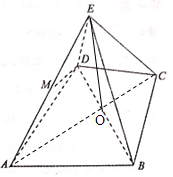 如图几何体E-ABCD是四棱锥,△ABD为正三角形,∠BCD=120°,CB=CD=CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD,
如图几何体E-ABCD是四棱锥,△ABD为正三角形,∠BCD=120°,CB=CD=CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com