
分析 本题利用几何概型求概率.先解绝对值不等式,再利用解得的区间长度与区间(-4,4)的长度求比值即得.
解答 解:利用几何概型,其测度为线段的长度.
由不等式|x-2|+|x+3|≥7可得
x≤-3,-x+2-x-3≥7,∴x≤-4;
-3<x<2,-x+2+x+3≥7,无解;
x≥2,x-2+x+3≥7,∴x≥3
故原不等式的解集为{x|x≤-4或x≥3},
∴在(-4,4)上随机取一个数x,则事件“|x-2|+|x+3|≥7成立”发生的概率为P=$\frac{4-3}{4+4}$=$\frac{1}{8}$.
故答案为$\frac{1}{8}$.
点评 本题主要考查了几何概型,简单地说,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.


科目:高中数学 来源: 题型:选择题
| A. | -64 | B. | -68 | C. | -70 | D. | -72 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
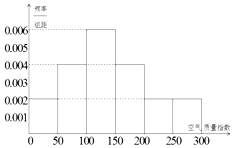 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
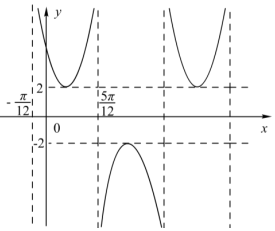 函数f (x )=$\frac{A}{sin(ωx+φ)}$ ( A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{4}$)=$\frac{4\sqrt{3}}{3}$.
函数f (x )=$\frac{A}{sin(ωx+φ)}$ ( A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{4}$)=$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1+2ln2}{4}$ | B. | $\frac{3-2ln2}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:选择题
幂函数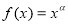 的图象经过点(2,4),则
的图象经过点(2,4),则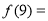 ( )
( )
A.1 B.3 C.9 D.81
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com