
【题目】已知函数![]() ,其中
,其中![]() 为实常数.
为实常数.
(1)若存在![]() ,使得
,使得![]() 在区间
在区间![]() 内单调递减,求
内单调递减,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,设直线
时,设直线![]() 与函数
与函数![]() 的图象相交于不同的两点
的图象相交于不同的两点![]() ,
,![]() ,证明:
,证明:![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某湿地公园内有一条河,现打算建一座桥将河两岸的路连接起来,剖面设计图纸如下:

其中,点![]() 为
为![]() 轴上关于原点对称的两点,曲线段
轴上关于原点对称的两点,曲线段![]() 是桥的主体,
是桥的主体,![]() 为桥顶,且曲线段
为桥顶,且曲线段![]() 在图纸上的图形对应函数的解析式为
在图纸上的图形对应函数的解析式为![]() ,曲线段
,曲线段![]() 均为开口向上的抛物线段,且
均为开口向上的抛物线段,且![]() 分别为两抛物线的顶点,设计时要求:保持两曲线在各衔接处(
分别为两抛物线的顶点,设计时要求:保持两曲线在各衔接处(![]() )的切线的斜率相等.
)的切线的斜率相等.
(1)求曲线段![]() 在图纸上对应函数的解析式,并写出定义域;
在图纸上对应函数的解析式,并写出定义域;
(2)车辆从![]() 经
经![]() 倒
倒![]() 爬坡,定义车辆上桥过程中某点
爬坡,定义车辆上桥过程中某点![]() 所需要的爬坡能力为:
所需要的爬坡能力为:![]() (该点
(该点![]() 与桥顶间的水平距离)
与桥顶间的水平距离)![]() (设计图纸上该点处的切线的斜率),其中
(设计图纸上该点处的切线的斜率),其中![]() 的单位:米.若该景区可提供三种类型的观光车:①游客踏乘;②蓄电池动力;③内燃机动力.它们的爬坡能力分别为
的单位:米.若该景区可提供三种类型的观光车:①游客踏乘;②蓄电池动力;③内燃机动力.它们的爬坡能力分别为![]() 米,
米,![]() 米,
米,![]() 米,又已知图纸上一个单位长度表示实际长度
米,又已知图纸上一个单位长度表示实际长度![]() 米,试问三种类型的观光车是否都可以顺利过桥?
米,试问三种类型的观光车是否都可以顺利过桥?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的的参数方程为
的的参数方程为![]() (其中
(其中![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() .曲线
.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 作直线
作直线![]() 的垂线交曲线
的垂线交曲线![]() 于
于![]() 两点(
两点(![]() 在
在![]() 轴上方),求
轴上方),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某搜索引擎广告按照付费价格对搜索结果进行排名,点击一次付费价格排名越靠前,被点击的次数也可能会提高,已知某关键词被甲、乙等多个公司竞争,其中甲、乙付费情况与每小时点击量结果绘制成如下的折线图.
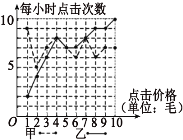
(1)若甲公司计划从这10次竞价中随机抽取3次竞价进行调研,其中每小时点击次数超过7次的竞价抽取次数记为![]() ,求
,求![]() 的分布列与数学期望;
的分布列与数学期望;
(2)若把乙公司设置的每次点击价格为x,每小时点击次数为![]() ,则点
,则点![]() 近似在一条直线附近.试根据前5次价格与每小时点击次数的关系,求y关于x的回归直线
近似在一条直线附近.试根据前5次价格与每小时点击次数的关系,求y关于x的回归直线![]() .(附:回归方程系数公式:
.(附:回归方程系数公式: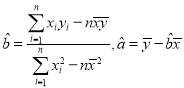
![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为研究学生语言学科的学习情况,现对高二200名学生英语和语文某次考试成绩进行抽样分析. 将200名学生编号为001,002,…,200,采用系统抽样的方法等距抽取10名学生,将10名学生的两科成绩(单位:分)绘成折线图如下:
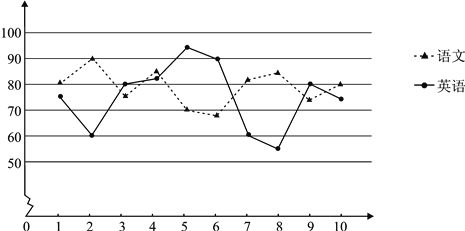
(Ⅰ)若第一段抽取的学生编号是006,写出第五段抽取的学生编号;
(Ⅱ)在这两科成绩差超过20分的学生中随机抽取2人进行访谈,求2人成绩均是语文成绩高于英语成绩的概率;
(Ⅲ)根据折线图,比较该校高二年级学生的语文和英语两科成绩,写出你的结论和理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() ,直线l不过原点O且不平行于坐标轴,l与E有两个交点A,B,线段AB的中点为M.
,直线l不过原点O且不平行于坐标轴,l与E有两个交点A,B,线段AB的中点为M.
![]() 若
若![]() ,点K在椭圆E上,
,点K在椭圆E上,![]() 、
、![]() 分别为椭圆的两个焦点,求
分别为椭圆的两个焦点,求![]() 的范围;
的范围;
![]() 证明:直线OM的斜率与l的斜率的乘积为定值;
证明:直线OM的斜率与l的斜率的乘积为定值;
![]() 若l过点
若l过点![]() ,射线OM与椭圆E交于点P,四边形OAPB能否为平行四边形?若能,求此时直线l斜率;若不能,说明理由.
,射线OM与椭圆E交于点P,四边形OAPB能否为平行四边形?若能,求此时直线l斜率;若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆上.
在椭圆上.
(1)求椭圆的方程;
(2)过椭圆的右焦点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() 、
、![]() ,其中直线
,其中直线![]() 交椭圆于
交椭圆于![]() 两点,直线
两点,直线![]() 交直线
交直线![]() 于
于![]() 点,求证:直线
点,求证:直线![]() 平分线段
平分线段![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 过点
过点![]() ,该抛物线的准线与椭圆
,该抛物线的准线与椭圆![]() :
:![]() 相切,且椭圆的离心率为
相切,且椭圆的离心率为![]() ,点
,点![]() 为椭圆
为椭圆![]() 的右焦点.
的右焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]()
![]() 两点,
两点,![]() 为平面上一定点,且满足
为平面上一定点,且满足![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com