
分析 直线l的方程为:$y=x+\frac{p}{2}$与抛物线方程联立可得根与系数的关系,利用弦长公式即可得出.
解答 证明:直线l的方程为:$y=x+\frac{p}{2}$…(2分)
联立方程组$\left\{{\begin{array}{l}{y=x+\frac{p}{2}}\\{{x^2}=2py}\end{array}}\right.$得:${y^2}-3py+\frac{p^2}{4}=0$…(8分)
设A(x1,y1),B(x2,y2),则由韦达定理知y1+y2=3p…(12分)
所以AB=AF+BF=y1+y2+p=4p为定值…(16分)
点评 本题考查了抛物线的标准方程及其性质、直线与抛物线相交转化为方程联立可得根与系数的关系、弦长公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若数列{an}是公差为1的等差数列,则数列{an+3} 是公差为4的等差数列 | |
| B. | 数列6,4,2,0 是公差为2的等差数列 | |
| C. | 若数列{an}等差,Sn是其前n项和,则数列$\{\frac{S_n}{n}\}$也等差 | |
| D. | 4与6的等差中项是±5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>0 | B. | 0<m<1 | C. | m>1 | D. | m>0且m≠1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
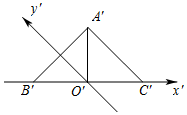 用斜二侧法画水平放置的△ABC的直观图,得到如图所示等腰直角△A′B′C′.已知点O′是斜边B′C′的中点,且A′O′=1,则△ABC的BC边上的高为( )
用斜二侧法画水平放置的△ABC的直观图,得到如图所示等腰直角△A′B′C′.已知点O′是斜边B′C′的中点,且A′O′=1,则△ABC的BC边上的高为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com