
【题目】已知三次函数![]() 过点
过点![]() ,且函数
,且函数![]() 在点
在点![]() 处的切线恰好是直线
处的切线恰好是直线![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ) 设函数![]() ,若函数
,若函数![]() 在区间
在区间![]() 上有两个零点,求实数
上有两个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)f(x)=x3﹣3x2(2)[﹣1,6).
【解析】分析:(1)根据已知条件即可建立关于b、c、d的三个方程,解方程即可求出b、c、d,从而求出函数![]() 的解析式;
的解析式;
(2)由已知条件得:f(x)﹣g(x)=0在[﹣2,1]上有两个不同的解,即x3﹣3x2﹣9x﹣m+1=0在区间[﹣2,1]有两个不同的解,即m=x3﹣3x2﹣9x+1在[﹣2,1]上有两个不同解,求函数x3﹣3x2﹣9x+1在区间[﹣2,1]上的取值范围,要使方程有两个不同的解,从而求出![]() 因满足的范围,这样便求出了
因满足的范围,这样便求出了![]() 的取值范围.
的取值范围.
详解:(1)f′(x)=3x2+2bx+c,由已知条件得:
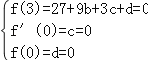 ,解得b=﹣3,c=d=0;
,解得b=﹣3,c=d=0;
∴f(x)=x3﹣3x2
(2)由已知条件得:f(x)﹣g(x)=0在[﹣2,1]上有两个不同的解;
即x3﹣3x2﹣9x﹣m+1=0在区间[﹣2,1]有两个不同的解;
即m=x3﹣3x2﹣9x+1在[﹣2,1]上有两个不同解.
令h(x)=x3﹣3x2﹣9x+1,h′(x)=3x2﹣6x﹣9,x∈[﹣2,1];
解3x2﹣6x﹣9>0得:﹣2≤x<﹣1;解3x2﹣6x﹣9<0得:﹣1<x≤1;
∴h(x)max=h(﹣1)=6,又f(﹣2)=﹣1,f(1)=﹣10,∴h(x)min=﹣10;
m=h(x)在区间[﹣2,1]上有两个不同的解,∴﹣1≤m<6.
∴实数m的取值范围是[﹣1,6).


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为圆
为圆![]() 上一动点,圆心
上一动点,圆心![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,点
,点![]() 分别是线段
分别是线段![]() 上的点,且
上的点,且![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 只有一个公共点
只有一个公共点![]() ,且点
,且点![]() 在第二象限,过坐标原点
在第二象限,过坐标原点![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为提高市民的戒烟意识,通过一个戒烟组织面向全市烟民征招志愿戒烟者,从符合条件的志愿者中随机抽取100名,将年龄分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,得到频率分布直方图如图所示.
五组,得到频率分布直方图如图所示.

(1)求图中![]() 的值,并估计这100名志愿者的平均年龄(同一组中的数据用该组区间的中点值作代表);
的值,并估计这100名志愿者的平均年龄(同一组中的数据用该组区间的中点值作代表);
(2)若年龄在![]() 的志愿者中有2名女性烟民,现从年龄在
的志愿者中有2名女性烟民,现从年龄在![]() 的志愿者中随机抽取2人,求至少有一名女性烟民的概率;
的志愿者中随机抽取2人,求至少有一名女性烟民的概率;
(3)该戒烟组织向志愿者推荐了![]() ,
,![]() 两种戒烟方案,这100名志愿者自愿选取戒烟方案,并将戒烟效果进行统计如下:
两种戒烟方案,这100名志愿者自愿选取戒烟方案,并将戒烟效果进行统计如下:
有效 | 无效 | 合计 | |
方案 | 48 | 60 | |
方案 | 36 | ||
合计 |
完成上面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为戒烟方案是否有效与方案选取有关.
的把握认为戒烟方案是否有效与方案选取有关.
参考公式:![]() ,
,![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两个桔柚(球形水果)种植基地,已知所有采摘的桔柚的直径都在![]() 范围内(单位:毫米,以下同),按规定直径在
范围内(单位:毫米,以下同),按规定直径在![]() 内为优质品,现从甲、乙两基地所采摘的桔柚中各随机抽取500个,测量这些桔柚的直径,所得数据整理如下:
内为优质品,现从甲、乙两基地所采摘的桔柚中各随机抽取500个,测量这些桔柚的直径,所得数据整理如下:
直径分组 |
|
|
|
|
|
|
|
甲基地频数 | 10 | 30 | 120 | 175 | 125 | 35 | 5 |
乙基地频数 | 5 | 35 | 115 | 165 | 110 | 60 | 10 |
(1)根据以上统计数据完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 以上的把握认为“桔柚直径与所在基地有关?”
以上的把握认为“桔柚直径与所在基地有关?”
甲基地 | 乙基地 | 合计 | |
优质品 | _________ | _________ | _________ |
非优质品 | _________ | _________ | _________ |
合计 | _________ | _________ | _________ |
(2)求优质品率较高的基地的500个桔柚直径的样本平均数![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(3)记甲基地直径在![]() 范围内的五个桔柚分别为
范围内的五个桔柚分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,现从中任取二个,求含桔柚
,现从中任取二个,求含桔柚![]() 的概率.
的概率.
附:![]() ,
,![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)过点M(m,2),其焦点为F,且|MF|=2.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设E为y轴上异于原点的任意一点,过点E作不经过原点的两条直线分别与抛物线C和圆F:(x﹣1)2+y2=1相切,切点分别为A,B,求证:直线AB过定点F(1,0).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两地生产某种产品,他们可以调出的数量分别为300吨、750吨.A,B,C三地需要该产品数量分别为200吨,450吨,400吨,甲地运往A,B,C三地的费用分别为6元/吨、3元/吨,5元/吨,乙地运往A,B,C三地的费用分别为5元/吨,9元/吨,6元/吨,问怎样调运,才能使总运费最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
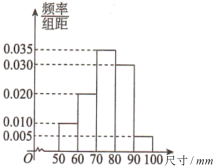
【题目】某工厂为检验车间一生产线工作是否正常,现从生产线中随机抽取一批零件样本,测量它们的尺寸(单位:![]() )并绘成频率分布直方图,如图所示.根据长期生产经验,可以认为这条生产线正常状态下生产的零件尺寸
)并绘成频率分布直方图,如图所示.根据长期生产经验,可以认为这条生产线正常状态下生产的零件尺寸![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为零件样本平均数
近似为零件样本平均数![]() ,
,![]() 近似为零件样本方差
近似为零件样本方差![]() .
.
(1)求这批零件样本的![]() 和
和![]() 的值(同一组中的数据用该组区间的中点值作代表);
的值(同一组中的数据用该组区间的中点值作代表);
(2)假设生产状态正常,求![]() ;
;
(3)若从生产线中任取一零件,测量其尺寸为![]() ,根据
,根据![]() 原则判断该生产线是否正常?
原则判断该生产线是否正常?
附:![]() ;若
;若![]() ,则
,则![]() ,
, ![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com