Question

18．据报我国正分别在大连和上海建造两航母，而建造航母必需特种钢．为建造航母的需要，要将两种不同的特种钢板截成A、B、C三种规格，每张钢板可同时截成三种规格的小钢板的块数如下表所示：

规格类型 钢板类型	A规格	B规格	C规格
第一种钢板	2	1	1
第二种钢板	1	2	3

今需要A、B、C三种规格的成品分别15、18、27块．问各截这两种钢板多少张可得所需三种规格成品，且使所用钢板张数最少？

Answer 1

分析 根据条件设第一种钢板x张，第二种钢板y张，钢板总数z张，建立约束条件和目标函数，利用线性规划的知识进行求解即可．

解答 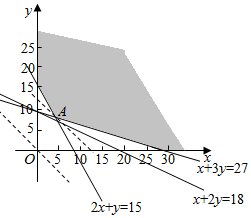解：设需要第一种钢板x张，第二种钢板y张，钢板总数z张，则$\left\{\begin{array}{l}2x+y≥15\\ x+2y≥18\\ x+3y≥27\\ x∈N，y∈N\end{array}\right.$目标函数 z=x+y
作出可行域如图所示，作出直线x+y=0．作出一组平行直线x+y=t（其中t为参数）．
其中经过可行域内的点且和原点距离最近的直线，
经过直线 x+3y=27和直线 2x+y=15的交点$A（\frac{18}{5}，\frac{39}{5}）$，直线方程为$x+y=\frac{57}{5}$．
由于$\frac{18}{5}$和$\frac{39}{5}$都不是整数，而最优解（x，y）中，x，y必须都是整数，
所以，可行域内点$A（\frac{18}{5}，\frac{39}{5}）$不是最优解．
经过可行域内的整点（横坐标和纵坐标都是整数的点），且与原点距离最近的直线是x+y=12．
经过的整点是B（3，9）和C（4，8），它们是最优解．
故要截得所需三种规格的钢板，且使所截两种钢板的张数最少的方法有两种，第一种截法是截第一种钢板3张、第二种钢板9张；第二种截法是截第一种钢板4张、第二种钢板8张．两种方法都最少要截两种钢板共12张．

点评 本题主要考查线性规划的应用，利用条件建立约束条件和目标函数，利用目标函数的几何意义求最优解，考查学生解决应用问题的能力．