
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在
在![]() 上有两个零点,求实数m的取值范围;
上有两个零点,求实数m的取值范围;
(3)若对区间![]() 内任意两个不等的实数
内任意两个不等的实数![]() ,
,![]() ,不等式
,不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)求出函数的导数,利用导数的几何意义即可求出函数![]() 在
在![]() 处的切线方程
处的切线方程
(2)先通过求导,研究函数![]() 的单调性,然后利用函数
的单调性,然后利用函数![]() 在
在![]() 上有两个零点可得直线
上有两个零点可得直线![]() 与
与![]() 的图像有两个交点,从而得到
的图像有两个交点,从而得到 ,求解即可
,求解即可
(3)不妨设![]() ,
,![]() 恒成立等价于
恒成立等价于![]() ,化简为
,化简为![]() ,然后,令
,然后,令![]() ,然后判断
,然后判断![]() 的单调性即可求解
的单调性即可求解
(1)当![]() 时,
时,![]() ,
,![]() ,切点坐标为
,切点坐标为![]() ,
,
切线的斜率![]() ,则切线方程为
,则切线方程为![]() ,即
,即![]() .
.
(2)![]() ,则
,则![]() ,
,
![]() ,故
,故![]() 时,
时,![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
故![]() 在
在![]() 处取得极大值
处取得极大值![]() .
.
又![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
![]() 在
在![]() 上的最小值是
上的最小值是![]() .
.
![]()
![]() 在
在![]() 上有两个零点的条件是
上有两个零点的条件是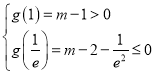
解得![]()
实数m的取值范围是![]()
(3)不妨设![]() ,
,![]() 恒成立等价于
恒成立等价于![]() ,即
,即![]() .
.
令![]() ,由
,由![]() ,
,![]() 具有任意性知,
具有任意性知,![]() 在区间
在区间![]() 内单调递减,
内单调递减,
![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
![]() ,
,![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,则
,则![]()
![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,
,
实数a的取值范围是![]()


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程:
的参数方程: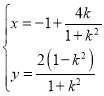 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)过曲线![]() 上一点
上一点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,中点为
两点,中点为![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+4[sin(θ+![]() )]x﹣2,θ∈[0,2π].
)]x﹣2,θ∈[0,2π].
(Ⅰ)若函数f(x)为偶函数,求tanθ的值;
(Ⅱ)若f(x)在[﹣![]() ,1]上是单调函数,求θ的取值范围.
,1]上是单调函数,求θ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 为平行四边形,
为平行四边形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 与
与![]() 所成的角为
所成的角为![]() ? 若存在,求出
? 若存在,求出![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 过点
过点![]() ,抛物线
,抛物线![]() 在
在![]() 处的切线交
处的切线交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 、
、![]() 分别与抛物线的准线交于点
分别与抛物线的准线交于点![]() 、
、![]() 、
、![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
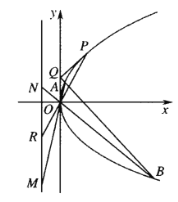
(Ⅰ)求抛物线![]() 的方程及其准线方程,并求出点
的方程及其准线方程,并求出点![]() 的坐标;
的坐标;
(Ⅱ)求证:![]() 为线段
为线段![]() 的中点.
的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与过其右焦点F(1,0)的直线交于不同的两点A,B,线段AB的中点为D,且直线l与直线OD的斜率之积为
与过其右焦点F(1,0)的直线交于不同的两点A,B,线段AB的中点为D,且直线l与直线OD的斜率之积为![]() .
.
(1)求C的方程;
(2)设椭圆的左顶点为M,kMA,kMB分别表示直线MA,MB的斜率,求证![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年9月25日.阿里巴巴在杭州云栖大会上正式对外发布了含光800AI芯片,在业界标准的ResNet -50测试中,含光800推理性能达到78563lPS,比目前业界最好的AI芯片性能高4倍;能效比500 IPS/W,是第二名的3.3倍.在国内集成电路产业发展中,集成电路设计产业始终是国内集成电路产业中最具发展活力的领域,增长也最为迅速.如图是2014-2018年中国集成电路设计产业的销售额(亿元)及其增速(%)的统计图,则下面结论中正确的是( )
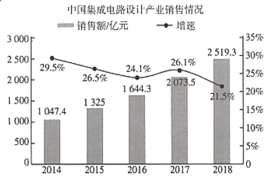
A.2014-2018年,中国集成电路设计产业的销售额逐年增加
B.2014-2017年,中国集成电路设计产业的销售额增速逐年下降
C.2018年中国集成电路设计产业的销售额的增长率比2015年的高
D.2018年与2014年相比,中国集成电路设计产业销售额的增长率约为110%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将曲线方程![]() ,先向左平移2个单位,再向上平移2个单位,得到曲线C.
,先向左平移2个单位,再向上平移2个单位,得到曲线C.
(1)点M(x,y)为曲线C上任意一点,写出曲线C的参数方程,并求出![]() 的最大值;
的最大值;
(2)设直线l的参数方程为![]() ,(t为参数),又直线l与曲线C的交点为E,F,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段EF的中点且与l垂直的直线的极坐标方程.
,(t为参数),又直线l与曲线C的交点为E,F,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段EF的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com