
【题目】在平面直角坐标系xOy中,将曲线方程![]() ,先向左平移2个单位,再向上平移2个单位,得到曲线C.
,先向左平移2个单位,再向上平移2个单位,得到曲线C.
(1)点M(x,y)为曲线C上任意一点,写出曲线C的参数方程,并求出![]() 的最大值;
的最大值;
(2)设直线l的参数方程为![]() ,(t为参数),又直线l与曲线C的交点为E,F,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段EF的中点且与l垂直的直线的极坐标方程.
,(t为参数),又直线l与曲线C的交点为E,F,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段EF的中点且与l垂直的直线的极坐标方程.
【答案】(1)![]() (θ为参数);4;(2)
(θ为参数);4;(2)![]()
【解析】
(1)直接利用转换关系,把参数方程极坐标方程和直角坐标方程之间进行转换,进一步利用三角函数关系式的变换和余弦型函数性质的应用求出结果.
(2)利用中点坐标公式的应用和直线垂直的充要条件的应用求出结果.
解:(1)将曲线方程![]() ,先向左平移2个单位,再向上平移2个单位,得到曲线C的方程为
,先向左平移2个单位,再向上平移2个单位,得到曲线C的方程为![]() ,
,
即![]() ,
,
故曲线C的参数方程为![]() (θ为参数);
(θ为参数);
又点M(x,y)为曲线C上任意一点,
所以![]() 2cos
2cos![]() 4cos(
4cos(![]() ).
).
所以![]() 的最大值为4;
的最大值为4;
(2)由(1)知曲线C的直角坐标方程为![]() ,
,
又直线l的参数方程为![]() ,(t为参数),
,(t为参数),
所以直线l的普通方程为x+2y﹣4=0,
所以有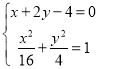 ,
,
解得![]() 或
或![]() .
.
所以线段EF的中点坐标为(![]() ),
),
即线段EF的中点坐标为(2,1),
直线l的斜率为![]() ,
,
则与直线l垂直的直线的斜率为2,
故所求直线的直角坐标方程为y﹣1=2(x﹣2),
即2x﹣y﹣3=0,
将x=ρcosθ,y=ρsinθ代入,
得其极坐标方程为2ρcosθ﹣ρsinθ﹣3=0.


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在
在![]() 上有两个零点,求实数m的取值范围;
上有两个零点,求实数m的取值范围;
(3)若对区间![]() 内任意两个不等的实数
内任意两个不等的实数![]() ,
,![]() ,不等式
,不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学从甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的众数是83,乙班学生成绩的平均数是86,则![]() 的值为( )
的值为( )
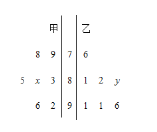
A.7B.8C.9D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() 分别是椭圆
分别是椭圆![]() :
:![]() (
(![]() )的左右焦点,点
)的左右焦点,点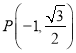 是椭圆
是椭圆![]() 上一点,且
上一点,且![]() .若椭圆
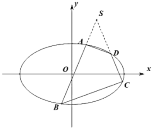
.若椭圆![]() 的内接四边形
的内接四边形![]() 的边
的边![]() 的延长线交于椭圆外一点
的延长线交于椭圆外一点![]() ,且点
,且点![]() 的横坐标为1,记直线
的横坐标为1,记直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,又函数![]() .
.
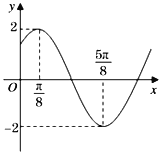
(1)求函数![]() 的单调减区间;
的单调减区间;
(2)设△ABC的内角A,B,C的对边分别为a,b,c,又![]() ,且锐角C满足
,且锐角C满足![]() ,若sinB=2sinA,求a+b的值.
,若sinB=2sinA,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为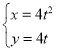 (其中t为参数).以坐标原点O为极点,x轴正半轴为极轴建立极坐标系并取相同的单位长度,曲线C2的极坐标方程为
(其中t为参数).以坐标原点O为极点,x轴正半轴为极轴建立极坐标系并取相同的单位长度,曲线C2的极坐标方程为![]() .
.
(1)把曲线C1的方程化为普通方程,C2的方程化为直角坐标方程;
(2)若曲线C1,C2相交于A,B两点,AB的中点为P,过点P做曲线C2的垂线交曲线C1于E,F两点,求|PE||PF|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AA1=2AB=2AD=4,过AA1作平面α使BD⊥α,且平面α∩平面A1B1C1D1=l,M∈l.下面给出了四个命题:这四个命题中,真命题的个数为( )
①l∥AC;
②BM⊥AC;
③l和AD1所成的角为60°;
④线段BM长度的最小值为![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小学的期末考试中抽取部分学生的数学成绩,由抽查结果得到如图的频率分布直方图,分数落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
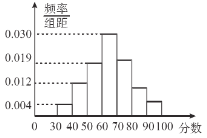
(1)求这些学生的分数落在区间![]() 内的频率;
内的频率;
(2)(ⅰ)若采用分层抽样的方法从分数落在区间![]() ,
,![]() 内抽取4人,求从分数落在区间
内抽取4人,求从分数落在区间![]() ,
,![]() 内各抽取的人数;
内各抽取的人数;
(ⅱ)从上述抽取的4人中再随机抽取2人,求这2人全部来自于区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,且直线
,且直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() .若直线
.若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,且
,且![]() 点为直线
点为直线![]() 上一点.
上一点.
(1)求![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 为椭圆
为椭圆![]() 的上顶点,直线
的上顶点,直线![]() 与
与![]() 轴交点
轴交点![]() ,记
,记![]() 表示面积,求
表示面积,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com