
 与销售额(单位:百万元)之间有如下对应数据:
与销售额(单位:百万元)之间有如下对应数据: | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 50 | 60 | 70 |
 与
与 之间具有线性相关关系.
之间具有线性相关关系. 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源:不详 题型:解答题
 和房屋面积
和房屋面积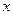 的有关数据:
的有关数据: 
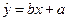 ,已计算得
,已计算得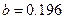 ,
,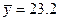 ,计算
,计算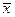 及
及 ;
; 的房屋销售价格.
的房屋销售价格.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
 必过点( )
必过点( )查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 序号 | 身高x | 脚长y | 序号 | 身高x | 脚长y |
| 1 | 176 | 42 | 11 | 179 | 44 |
| 2 | 175 | 44 | 12 | 169 | 43 |
| 3 | 174 | 41 | 13 | 185 | 45 |
| 4 | 180 | 44 | 14 | 166 | 40 |
| 5 | 170 | 42 | 15 | 174 | 42 |
| 6 | 178 | 43 | 16 | 167 | 42 |
| 7 | 173 | 42 | 17 | 173 | 41 |
| 8 | 168 | 40 | 18 | 174 | 42 |
| 9 | 190 | 46 | 19 | 172 | 42 |
| 10 | 171 | 42 | 20 | 175 | 41 |
| | 高个 | 非高个 | 合计 |
| 大脚 | | | |
| 非大脚 | | 12 | |
| 合计 | | | 20 |
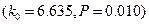
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的
的 前六项。
前六项。 学生,试估计该校新生的近视率
学生,试估计该校新生的近视率 的大
的大
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
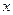 ,数学成绩为
,数学成绩为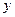 (注:没有相同姓名的学生).
(注:没有相同姓名的学生).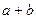 的值;
的值; 的概率;
的概率;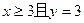 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 分)有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表
分)有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表| | 不及格 | 及格 | 总计 |
| 甲班 | 10 | 35 | M |
| 乙班 | 7 | 38 | 45 |
| 总计 | 17 | 73 | N |
 观测值的计算式
观测值的计算式 =0.6527你有多大把握认为成绩及格与班级
=0.6527你有多大把握认为成绩及格与班级 有关?
有关? =7.121又说明什么?
=7.121又说明什么?
 )
) 0.100,P(k
0.100,P(k
 )
) 0.010)
0.010)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | 色盲 | 不色盲 | 合计 |
| 男 | 15 | 20 | 35 |
| 女 | 12 | 8 | 20 |
| 合计 | 27 | 28 | 55 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.根据2×2列联表中的数据计算得出K2≥6.635, 而P(K2≥6.635)≈0.01,则有99% 的把握认为两个分类变量有关系 |
| B.在线性回归分析中,相关系数为r,|r|越接近于1,相关程度越大;|r|越小,相关程度越小 |
| C.在回归分析中,相关指数R2越大,说明残差平方和越小,回归效果越好 |
D.在回归直线 中,变量x=200时,变量y的值一定是15 中,变量x=200时,变量y的值一定是15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com