
分析 通过零点分段去掉绝对值,确定函数的解析式,通过图象分析,解决恒成立问题.
解答 解:f(x)=$\left\{\begin{array}{l}{-x}&{0≤x<\frac{m}{3}}\\{-\frac{m}{3}}&{\frac{m}{3}≤x<\frac{2m}{3}}\\{x-m}&{x≥\frac{2m}{3}}\end{array}\right.$,由奇函数的图象特点,画出函数图象,
若对任意的实数x,都有f(x-1)≤f(x)成立的含义为f(x)的图象向右平移一个单位以后图象恒在f(x)的下方或相等.
只需2m≤1,则0<m≤$\frac{1}{2}$,
故答案为:$0<m≤\frac{1}{2}$.
点评 本题考查了函数的奇偶性及函数的平移,同时考查了数形结合的数学思想.对于学生灵活解决恒成立问题有很大的帮助.


科目:高中数学 来源: 题型:选择题
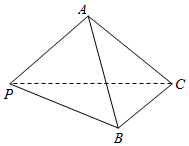 已知在三棱锥P-ABC中,VP-ABC=$\frac{{4\sqrt{3}}}{3}$,∠APC=$\frac{π}{4}$,∠BPC=$\frac{π}{3}$,PA⊥AC,PB⊥BC,且平面PAC⊥平面PBC,那么三棱锥P-ABC外接球的体积为( )
已知在三棱锥P-ABC中,VP-ABC=$\frac{{4\sqrt{3}}}{3}$,∠APC=$\frac{π}{4}$,∠BPC=$\frac{π}{3}$,PA⊥AC,PB⊥BC,且平面PAC⊥平面PBC,那么三棱锥P-ABC外接球的体积为( )| A. | $\frac{4π}{3}$ | B. | $\frac{{8\sqrt{2}π}}{3}$ | C. | $\frac{{12\sqrt{3}π}}{3}$ | D. | $\frac{32π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com