
分析 x+y+z=9,xy+yz+xz=24,可得:x+y=9-z,xy=24-z(9-z)=24-9z+z2.因此x,y是一元二次方程t2-(9-z)t+24-9z+z2=0的两个实数根,利用△≥0.可得z的取值范围,则$\frac{{x}^{2}+{y}^{2}}{z}$=$\frac{(x+y)^{2}-2xy}{z}$=$\frac{33-{z}^{2}}{z}$,利用导数研究其单调性极值与最值即可得出.
解答 解:x+y+z=9,xy+yz+xz=24,
∴x+y=9-z,
xy=24-z(9-z)=24-9z+z2.
∴x,y是一元二次方程t2-(9-z)t+24-9z+z2=0的两个实数根,
∴△=(9-z)2-4(24-9z+z2)≥0.
化为:z2-6z+5≤0,解得1≤z≤5.
则$\frac{{x}^{2}+{y}^{2}}{z}$=$\frac{(x+y)^{2}-2xy}{z}$=$\frac{(9-z)^{2}-2(24-9z+{z}^{2})}{z}$=$\frac{33-{z}^{2}}{z}$=f(z),
f′(z)=$-\frac{33}{{z}^{2}}$-1<0,
∴f(z)在[1,5]上单调递减,
∴f(z)∈$[\frac{8}{5},32]$.
故答案为:$[\frac{8}{5},32]$.
点评 本题考查了一元二次方程的根与系数的关系、利用导数研究函数的单调性极值与最值、不等式的解法,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
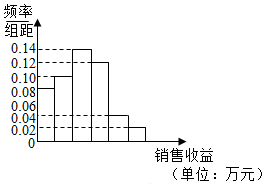 某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费,并将各地的销售收益绘制成频率分布直方图(如图所示),由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费,并将各地的销售收益绘制成频率分布直方图(如图所示),由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.| 广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
| 销售收益y(单位:万元) | 2 | 3 | 2 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{(5π-6\sqrt{3})^{2}}{18}$ | B. | $\frac{(5π+6\sqrt{3})^{2}}{18}$ | C. | $\frac{{π}^{2}}{18}$ | D. | $\frac{{π}^{2}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当x>0且x≠1时,lgx+$\frac{1}{lgx}$≥2 | |
| B. | 当x>0时,$\sqrt{x}$+$\frac{1}{\sqrt{x}}$≥2 | |
| C. | 当0<θ≤$\frac{π}{2}$时,sinθ+$\frac{2}{sinθ}$的最小值为2$\sqrt{2}$ | |
| D. | 当-$\frac{1}{2}$≤x<0时,x+$\frac{1}{x}$有最大值-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π | B. | 2$\sqrt{6}$π | C. | 6π | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com