
分析 (1)通过对${a_n}=\frac{{3n{a_{n-1}}}}{{2{a_{n-1}}+n-1}}(n≥2,n∈N)$变形可知$\frac{n}{a_n}-1=\frac{1}{3}(\frac{n-1}{{{a_{n-1}}}}-1)$,进而计算可得结论;
(2)当n≥2时通过放缩可知$\frac{{3}^{n}}{{3}^{n}-1}$≤1+$\frac{1}{8×{3}^{n-2}}$,进而利用分组求和法计算即得结论.
解答 (1)解:∵${a_n}=\frac{{3n{a_{n-1}}}}{{2{a_{n-1}}+n-1}}(n≥2,n∈N)$,
∴$\frac{n}{a_n}=\frac{n-1}{{3{a_{n-1}}}}+\frac{2}{3}$,即$\frac{n}{a_n}-1=\frac{1}{3}(\frac{n-1}{{{a_{n-1}}}}-1)$,
所以数列$\{\frac{n}{a_n}-1\}$是以$\frac{1}{a_1}-1$为首项、$\frac{1}{3}$为公比的等比数列,
又∵a1=$\frac{3}{2}$,
∴$\frac{n}{a_n}-1=-{(\frac{1}{3})^n}$,即${a_n}=\frac{{n{3^n}}}{{{3^n}-1}}$;
(2)证明:当n≥2时,$\frac{3^n}{{{3^n}-1}}=\frac{{{3^n}-1+1}}{{{3^n}-1}}=1+\frac{1}{{{3^n}-1}}≤1+\frac{1}{{{3^n}(1-\frac{1}{3^n})}}≤1+\frac{1}{{{3^n}(1-\frac{1}{3^2})}}≤1+\frac{9}{{8×{3^n}}}=1+\frac{1}{{8×{3^{n-2}}}}$,
$\begin{array}{l}\frac{a_1}{1}+\frac{a_2}{2}+\frac{a_3}{3}+…+\frac{a_n}{n}-n\\=\frac{3}{{{3^1}-1}}+\frac{3^2}{{{3^2}-1}}+\frac{3^3}{{{3^3}-1}}+…+\frac{3^n}{{{3^n}-1}}-n\end{array}$
=$(1+\frac{1}{{{3^1}-1}})+(1+\frac{1}{{{3^2}-1}})+(1+\frac{1}{{{3^3}-1}})+(1+\frac{1}{{{3^4}-1}})…+(1+\frac{1}{{{3^n}-1}})-n$
$≤\frac{1}{2}+\frac{1}{8}+\frac{1}{8×3}+\frac{1}{{8×{3^2}}}+…+\frac{1}{{8×{3^{n-2}}}}$
=$\frac{1}{2}+\frac{{\frac{1}{8}(1-{{(\frac{1}{3})}^{n-1}})}}{{1-\frac{1}{3}}}$
$≤\frac{1}{2}+\frac{3}{16}$=$\frac{11}{16}$.
点评 本题是一道关于数列与不等式的综合题,考查放缩法、分组求和法,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
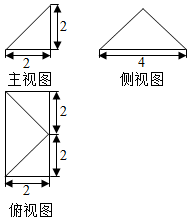
| A. | 4 | B. | $\frac{16}{3}$ | C. | 8 | D. | $\frac{32}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com