
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)![]() 为曲线
为曲线![]() 上任一点,过点
上任一点,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() (
(![]() 为切点),求
为切点),求![]() 的最小值.
的最小值.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】关于数列有下列命题:
①数列{an}的前n项和为Sn , 且Sn=an﹣1(a∈R),则{an}为等差或等比数列;
②数列{an}为等差数列,且公差不为零,则数列{an}中不会有am=an(m≠n),
③一个等差数列{an}中,若存在ak+1>ak>0(k∈N*),则对于任意自然数n>k,都有an>0;
④一个等比数列{an}中,若存在自然数k,使akak+1<0,则对于任意n∈N* , 都有anan+1<0,
其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机床厂今年初用98万元购进一台数控机床,并立即投入使用,计划第一年维修、保养费用12万元,从第二年开始,每年的维修、保养修费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利总额y元.
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利?
(3)使用若干年后,对机床的处理有两种方案:①当年平均盈利额达到最大值时,以30万元价格处理该机床;②当盈利额达到最大值时,以12万元价格处理该机床.问哪种方案处理较为合理?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二次函数f(x)=x2+bx+c(b,c∈R),f(1)=0,且1≤x≤3时,f(x)≤0恒成立,f(x)是区间[2,+∞)上的增函数.函数f(x)的解析式是;若|f(m)|=|f(n)|,且m<n<2,u=m+n,u的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
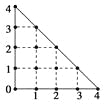
【题目】某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示:
X | 1 | 2 | 3 | 4 |
Y | 51 | 48 | 45 | 42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(2)从所种作物中随机选取一株,求它的年收获量的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,AB⊥BC侧面PAB⊥底面ABCD,PA=AD=AB=2,BC=4. 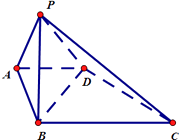
(1)若PB中点为E.求证:AE∥平面PCD;
(2)若∠PAB=60°,求直线BD与平面PCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列,数学期望及方差;
(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1,a32=9a2a6 .
(1)求数列{an}的通项公式;
(2)设bn=|10+2log3an|,求数列{bn}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com