
【题目】在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,AB⊥BC侧面PAB⊥底面ABCD,PA=AD=AB=2,BC=4. 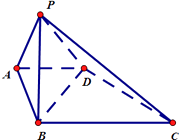
(1)若PB中点为E.求证:AE∥平面PCD;
(2)若∠PAB=60°,求直线BD与平面PCD所成角的正弦值.
【答案】
(1)证明:如图,取PC的中点F,连结DF,EF;
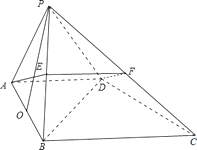
∵EF∥AD,且AD=EF,所以ADFE为平行四边形;
∴AE∥DF,且AE平面PCD,DF平面PCD;
∴AE∥平面PCD
(2)解:∵∠PAB=60°,PA=AB;
∴△PAB为等边三角形,取AB中点O,连接PO;
则PO⊥AB;
又侧面PAB⊥底面ABCD,平面PAB∩平面ABCD=AB;
∴PO⊥平面ABCD;
根据已知条件可求得PO= ![]() ,S△BCD=4,PD=CD=
,S△BCD=4,PD=CD= ![]() ,PC=2
,PC=2 ![]() ,
, ![]() ;
;
设点B到平面PCD的距离为h;
∴ ![]() ,
, ![]() ;
;
∵VP﹣BCD=VB﹣PCD;
∴ ![]() ;
;
∴直线BD与平面PCD所成角θ的正弦值 ![]()
【解析】(1)取PC中点F,并连接DF,FE,根据已知条件容易说明四边形ADFE为平行四边形,从而有AE∥DF,根据线面平行的判定定理即得到AE∥平面PCD;(2)设B到平面PCD的距离为h,从而直线BD与平面PCD所成角的正弦值便可表示为 ![]() ,BD根据已知条件容易求出,而求h可通过VP﹣BCD=VB﹣PCD求出:取AB中点O,连接PO,可以说明PO⊥平面ABCD,而根据已知条件能够求出S△BCD , S△PCD , 从而求出h,从而求得答案.
,BD根据已知条件容易求出,而求h可通过VP﹣BCD=VB﹣PCD求出:取AB中点O,连接PO,可以说明PO⊥平面ABCD,而根据已知条件能够求出S△BCD , S△PCD , 从而求出h,从而求得答案.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则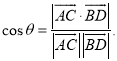 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=1,an+1=1﹣ ![]() ,bn=
,bn= ![]() ,其中n∈N* .
,其中n∈N* .
(1)求证:数列{bn}为等差数列;
(2)设cn=bn+1( ![]() )
) ![]() ,数列{cn}的前n项和为Tn , 求Tn;
,数列{cn}的前n项和为Tn , 求Tn;
(3)证明:1+ ![]() +
+ ![]() +…+
+…+ ![]() ≤2
≤2 ![]() ﹣1(n∈N*)
﹣1(n∈N*)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)![]() 为曲线
为曲线![]() 上任一点,过点
上任一点,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() (
(![]() 为切点),求
为切点),求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且和直线
且和直线![]() 相切,记动圆的圆心
相切,记动圆的圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设曲线![]() 上一点
上一点![]() 的横坐标为
的横坐标为![]() ,过
,过![]() 的直线交
的直线交![]() 于一点
于一点![]() ,交
,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于另一点
于另一点![]() ,若
,若![]() 是
是![]() 的切线,求
的切线,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某特色餐馆开通了美团外卖服务,在一周内的某特色菜外卖份数![]() (份)与收入
(份)与收入![]() (元)之间有如下的对应数据:
(元)之间有如下的对应数据:
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计外卖份数为12份时,收入为多少元.
注:①参考公式:线性回归方程系数公式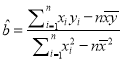 ,
, ![]() ;
;
②参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点. 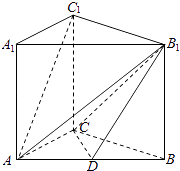
(1)求证:AC1∥平面CDB1
(2)求证:AC⊥BC1
(3)求直线AB1与平面BB1C1C所成的角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com