
【题目】在数列{an}中,a1=1,an+1=1﹣ ![]() ,bn=
,bn= ![]() ,其中n∈N* .
,其中n∈N* .
(1)求证:数列{bn}为等差数列;
(2)设cn=bn+1( ![]() )
) ![]() ,数列{cn}的前n项和为Tn , 求Tn;
,数列{cn}的前n项和为Tn , 求Tn;
(3)证明:1+ ![]() +
+ ![]() +…+
+…+ ![]() ≤2
≤2 ![]() ﹣1(n∈N*)
﹣1(n∈N*)
【答案】
(1)证明:bn+1﹣bn= ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() =1,又b1=1.∴数列{bn}为等差数列,首项为1,公差为1
=1,又b1=1.∴数列{bn}为等差数列,首项为1,公差为1
(2))解:由(1)可得:bn=n.
cn=bn+1( ![]() )
) ![]() =(n+1)
=(n+1) ![]() .
.
∴数列{cn}的前n项和为Tn= ![]() +3×
+3× ![]() +
+ ![]() +…+(n+1)
+…+(n+1) ![]() .
.
![]() =
= ![]() +3×
+3× ![]() +…+n
+…+n ![]() +(n+1)
+(n+1) ![]() ,
,
∴ ![]() Tn=
Tn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ﹣(n+1)
﹣(n+1) ![]() =
= ![]() +
+ ![]() ﹣(n+1)
﹣(n+1) ![]() ,
,
可得Tn= ![]() ﹣
﹣ ![]()
(3)证明:1+ ![]() +
+ ![]() +…+
+…+ ![]() ≤2
≤2 ![]() ﹣1(n∈N*)即为:1+
﹣1(n∈N*)即为:1+ ![]() +
+ ![]() +…+
+…+ ![]() ≤2
≤2 ![]() ﹣1.
﹣1.
∵ ![]() =
= ![]() <
< ![]() =2
=2 ![]() (k=2,3,…).
(k=2,3,…).
∴1+ ![]() +
+ ![]() +…+
+…+ ![]() ≤1+2[(
≤1+2[( ![]() ﹣1)+(
﹣1)+( ![]() )+…+(
)+…+( ![]() ﹣
﹣ ![]() )]=1+2
)]=1+2 ![]() =2
=2 ![]() ﹣1.
﹣1.
∴1+ ![]() +
+ ![]() +…+
+…+ ![]() ≤2
≤2 ![]() ﹣1(n∈N*)
﹣1(n∈N*)
【解析】(1)只要证明bn+1﹣bn= ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() ,为常数.(2)由(1)可得:bn=n.cn=bn+1(
,为常数.(2)由(1)可得:bn=n.cn=bn+1( ![]() )
) ![]() =(n+1)
=(n+1) ![]() .利用“错位相减法”与等比数列的求和公式即可得出.(3)1+
.利用“错位相减法”与等比数列的求和公式即可得出.(3)1+ ![]() +
+ ![]() +…+
+…+ ![]() ≤2
≤2 ![]() ﹣1(n∈N*)即为:1+
﹣1(n∈N*)即为:1+ ![]() +
+ ![]() +…+
+…+ ![]() ≤2
≤2 ![]() ﹣1.由于
﹣1.由于 ![]() =
= ![]() <
< ![]() =2
=2 ![]() (k=2,3,…).利用“裂项求和方法”即可得出.
(k=2,3,…).利用“裂项求和方法”即可得出.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系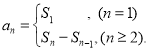 ),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且满足c cosB=(2a+b)cos(π﹣C).
(1)求角C的大小;
(2)若c=4,△ABC的面积为![]() ,求a+b的值
,求a+b的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,若 ![]() (acosB+bcosA)=2csinC,a+b=8,且△ABC的面积的最大值为4
(acosB+bcosA)=2csinC,a+b=8,且△ABC的面积的最大值为4 ![]() ,则此时△ABC的形状为( )
,则此时△ABC的形状为( )
A.等腰三角形
B.正三角形
C.直角三角形
D.钝角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中,a1=1,且a2+2,a3 , a4﹣2成等比数列.
(1)求数列{an}的通项公式;
(2)若bn= ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机床厂今年初用98万元购进一台数控机床,并立即投入使用,计划第一年维修、保养费用12万元,从第二年开始,每年的维修、保养修费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利总额y元.
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利?
(3)使用若干年后,对机床的处理有两种方案:①当年平均盈利额达到最大值时,以30万元价格处理该机床;②当盈利额达到最大值时,以12万元价格处理该机床.问哪种方案处理较为合理?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
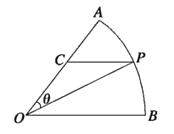
【题目】如图所示,扇形![]() ,圆心角
,圆心角![]() 的大小等于
的大小等于![]() ,半径为2,在半径
,半径为2,在半径![]() 上有一动点
上有一动点![]() ,过点
,过点![]() 作平行于
作平行于![]() 的直线交弧
的直线交弧![]() 于点
于点![]() .
.
(1)若![]() 是半径
是半径![]() 的中点,求线段
的中点,求线段![]() 的大小;
的大小;
(2)设![]() ,求
,求![]() 面积的最大值及此时
面积的最大值及此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二次函数f(x)=x2+bx+c(b,c∈R),f(1)=0,且1≤x≤3时,f(x)≤0恒成立,f(x)是区间[2,+∞)上的增函数.函数f(x)的解析式是;若|f(m)|=|f(n)|,且m<n<2,u=m+n,u的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,AB⊥BC侧面PAB⊥底面ABCD,PA=AD=AB=2,BC=4. 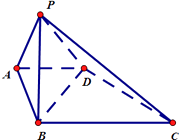
(1)若PB中点为E.求证:AE∥平面PCD;
(2)若∠PAB=60°,求直线BD与平面PCD所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com