练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知随机变量ξ的概率分布如下，则P（ξ=10）=（ ）

    ξ

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    P

    m


    A.
    B.
    C.
    D.

    【答案】C
    【解析】解：∵由题意知，本题需要先计算出其它的概率之和，
    ∴根据表格可以看出9个变量对应的概率组成一个首项是 ，公比是 的等比数列，
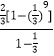    ∴S= =1﹣ ，
    ∵S+m=1，
    ∴m= ，
    故选C．
    【考点精析】解答此题的关键在于理解离散型随机变量及其分布列的相关知识，掌握在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某高校在今年的自主招生考试成绩中随机抽取100名考生的笔试成绩，分为5组制出频率分布直方图如图所示.

    （1）求的值；

    （2）该校决定在成绩较好的3、4、5组用分层抽样抽取6名学生进行面试，则每组应各抽多少名学生？

    （3）在（2）的前提下，已知面试有4位考官，被抽到的6名学生中有两名被指定甲考官面试，其余4名则随机分配给3位考官中的一位对其进行面试，求这4名学生分配到的考官个数的分布列和期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}中，a1=1，且a2+2，a3 ， a4﹣2成等比数列．
    （1）求数列{an}的通项公式；
    （2）若bn= ，求数列{bn}的前n项和Sn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

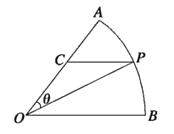
    【题目】如图所示，扇形，圆心角的大小等于，半径为2，在半径上有一动点，过点作平行于的直线交弧于点.

    （1）若是半径的中点，求线段的大小；

    （2）设，求面积的最大值及此时的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设二次函数f（x）=x2+bx+c（b，c∈R），f（1）=0，且1≤x≤3时，f（x）≤0恒成立，f（x）是区间[2，+∞）上的增函数．函数f（x）的解析式是；若|f（m）|=|f（n）|，且m＜n＜2，u=m+n，u的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）= ，a＜b＜c，且f（a）=f（b）=f（c）=0，现给出如下结论：①f（0）f（1）＞0；②f（0）f（1）＜0；③f（0）f（2）＞0；④f（0）f（2）＜0．其中正确结论的序号为（ ）
    A.①③
    B.①④
    C.②④
    D.②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD∥BC，AB⊥BC侧面PAB⊥底面ABCD，PA=AD=AB=2，BC=4．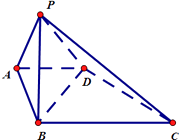

    （1）若PB中点为E．求证：AE∥平面PCD；
    （2）若∠PAB=60°，求直线BD与平面PCD所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列命题：

    ① “若，则有实根”的逆否命题为真命题；

    ②命题“”为真命题的一个充分不必要条件是；

    ③命题“，使得”的否定是真命题；

    ④命题函数为偶函数，命题函数在上为增函数，

    则为真命题.

    其中，正确的命题是（ ）

    A. ①② B. ①③ C. ②③ D. ③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= 的定义域为A．
    （1）求A；
    （2）已知k＞0，集合B={x| }，且A∩B≠，求实数k的取值范围．

    查看答案和解析>>

    同步练习册答案