
| A. | 若m⊥α,m⊥β,则α∥β | B. | 若m∥n,m⊥α,则n⊥α | ||
| C. | 若m⊥α,m?β,则α⊥β | D. | 若m∥α,α∩β=n,则m∥n |
科目:高中数学 来源: 题型:选择题
 把一个底面边长和高都为6的正三棱锥(底面是正三角形,从顶点向底面作垂线,垂足是底面的中心的三棱锥)P-ABC的底面ABC放置在平面α上,现让三棱锥绕棱BC逆时针方向旋转,使侧面PBC落在α内,则在旋转过程中正三棱锥P-ABC在α上的正投影图的面积取值范围是( )
把一个底面边长和高都为6的正三棱锥(底面是正三角形,从顶点向底面作垂线,垂足是底面的中心的三棱锥)P-ABC的底面ABC放置在平面α上,现让三棱锥绕棱BC逆时针方向旋转,使侧面PBC落在α内,则在旋转过程中正三棱锥P-ABC在α上的正投影图的面积取值范围是( )| A. | [$\frac{54\sqrt{13}}{13}$,12$\sqrt{3}$] | B. | [$\frac{54\sqrt{13}}{13}$,9$\sqrt{3}$] | C. | [$\frac{48\sqrt{13}}{13}$,12$\sqrt{3}$] | D. | [$\frac{48\sqrt{13}}{13}$,3$\sqrt{39}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 在校英语节演讲比赛中,七位评委老师为某班选手打出的分数的茎叶图(如图所示),去掉一个最高分和一个最低分后,所剩数据的方差为$\frac{8}{5}$.
在校英语节演讲比赛中,七位评委老师为某班选手打出的分数的茎叶图(如图所示),去掉一个最高分和一个最低分后,所剩数据的方差为$\frac{8}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
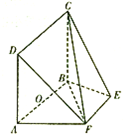 如图,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在平面与平面ABEF互相垂直.
如图,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在平面与平面ABEF互相垂直.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com