
分析 (1)求出导数,得到f(x)为周期为4的函数,即可得到所求的解析式;
(2)设g(x)=1+sinx-ax-cosx,求出导数,运用正弦函数的值域,讨论①当a≤-1时,②当a≥$\sqrt{2}$时,③当-1<a<$\sqrt{2}$时,由函数的单调性和不等式恒成立的思想,求得最小值,解不等式即可得到所求范围;
(3)由(2)可得x∈[0,π],sinx-cosx≥$\frac{2}{π}$x-1,即有$\sqrt{2}$sin(x-$\frac{π}{4}$)≥$\frac{2}{π}$x-1,当1≤k≤n+1时,0≤$\frac{kπ}{2n+1}$+$\frac{π}{4}$≤π,$\sqrt{2}$sin$\frac{kπ}{2n+1}$=$\sqrt{2}$sin($\frac{kπ}{2n+1}$+$\frac{π}{4}$-$\frac{π}{4}$)≥$\frac{2}{π}$($\frac{kπ}{2n+1}$+$\frac{π}{4}$)-1=$\frac{2k}{2n+1}$-$\frac{1}{2}$,由累加法和等差数列的求和公式,计算即可得证.
解答 解:(1)f1(x)=cosx,f2(x)=-sinx,
f3(x)=-cosx,f4(x)=sinx,…,
f(x)为周期为4的函数,
即有f2015(x)=f4×503+3(x)=f3(x)=-cosx;
(2)设g(x)=1+sinx-ax-cosx,
g′(x)=cosx-a+sinx=$\sqrt{2}$sin(x$+\frac{π}{4}$)-a,
由x∈[0,π],即有$\sqrt{2}$sin(x$+\frac{π}{4}$)∈[-1,$\sqrt{2}$],
①当a≤-1时,g′(x)≥0在[0,π]恒成立,g(x)递增,
即有g(x)的最小值为g(0)=0,则a≤-1;
②当a≥$\sqrt{2}$时,g′(x)≤0在[0,π]恒成立,g(x)递减,
即有g(x)的最小值为g(π)=2-aπ,由g(π)≥0可得a≤$\frac{2}{π}$,舍去;
③当-1<a<$\sqrt{2}$时,存在x0∈[0,π],使得x∈(0,x0)g(x)递增,x∈(x0,π)时,g(x)递减.
g(x)min=min{g(0),g(π)},由$\left\{\begin{array}{l}{g(0)≥0}\\{g(π)≥0}\end{array}\right.$可得a≤$\frac{2}{π}$,则有-1<a≤$\frac{2}{π}$.
综上可得,a的取值范围是(-∞,$\frac{2}{π}$];
(3)证明:由(2)可得x∈[0,π],sinx+1≥$\frac{2}{π}$x+cosx,
即sinx-cosx≥$\frac{2}{π}$x-1,即有$\sqrt{2}$sin(x-$\frac{π}{4}$)≥$\frac{2}{π}$x-1,
当1≤k≤n+1时,0≤$\frac{kπ}{2n+1}$+$\frac{π}{4}$≤π,
即有$\sqrt{2}$sin$\frac{kπ}{2n+1}$=$\sqrt{2}$sin($\frac{kπ}{2n+1}$+$\frac{π}{4}$-$\frac{π}{4}$)≥$\frac{2}{π}$($\frac{kπ}{2n+1}$+$\frac{π}{4}$)-1=$\frac{2k}{2n+1}$-$\frac{1}{2}$,
则$\sqrt{2}$[f($\frac{π}{2n+1}$)+f($\frac{2π}{2n+1}$)+…+f($\frac{(n+1)π}{2n+1}$)]≥$\frac{2}{2n+1}$-$\frac{1}{2}$+$\frac{4}{2n+1}$-$\frac{1}{2}$+$\frac{2(n+1)}{2n+1}$-$\frac{1}{2}$
=$\frac{2}{2n+1}$•$\frac{1}{2}$(n+1)(n+2)-$\frac{1}{2}$(n+1)=$\frac{3}{2}$•$\frac{n+1}{2n+1}$.
即为f($\frac{π}{2n+1}$)+f($\frac{2π}{2n+1}$)+…+f($\frac{(n+1)π}{2n+1}$)≥$\frac{{3\sqrt{2}(n+1)}}{4(2n+1)}$.
点评 本题考查导数的运用:求单调区间和极值、最值,同时考查函数的周期性及运用,运用分类讨论的思想方法和函数单调性的运用,结合正弦函数的值域,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥α,m⊥β,则α∥β | B. | 若m∥n,m⊥α,则n⊥α | ||
| C. | 若m⊥α,m?β,则α⊥β | D. | 若m∥α,α∩β=n,则m∥n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
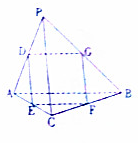 如图,已知三棱锥P-ABC中,点D,E,F,G分别是棱AP,AC,BC,PB上的点,若PA=PB=PC=$\sqrt{2}$,AB=AC=BC=1,且$\frac{AE}{AC}$=$\frac{AD}{AP}$=$\frac{BF}{BC}$=$\frac{BG}{BP}$.
如图,已知三棱锥P-ABC中,点D,E,F,G分别是棱AP,AC,BC,PB上的点,若PA=PB=PC=$\sqrt{2}$,AB=AC=BC=1,且$\frac{AE}{AC}$=$\frac{AD}{AP}$=$\frac{BF}{BC}$=$\frac{BG}{BP}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com