
分析 g(x)≠0,f(x)g(x)=h(x),h′(x)g(x)≥h(x)g′(x),可得$f(x)=\frac{h(x)}{g(x)}$,f′(x)≥0,于是f(x)在R上单调递增.由f(0)=0,f(1-x)=1-f(x),可得f(1)=1,因此f($\frac{1}{3}$)=$\frac{1}{2}$,$f(\frac{2}{3})$=$\frac{1}{2}$.必然有当$\frac{1}{3}≤x≤\frac{2}{3}$时,f(x)=$\frac{1}{2}$.可得$f(\frac{2}{5})=f(\frac{7}{15})=\frac{1}{2}$,即可得出.
解答 解:∵g(x)≠0,f(x)g(x)=h(x),h′(x)g(x)≥h(x)g′(x),
∴$f(x)=\frac{h(x)}{g(x)}$,${f}^{′}(x)=\frac{{h}^{′}(x)g(x)-h(x){g}^{′}(x)}{{g}^{2}(x)}$≥0,
∴f(x)在R上单调递增.
∵f(0)=0,f(1-x)=1-f(x),∴f(1-0)=1-f(0),∴f(1)=1,
∴f($\frac{1}{3}$)=$\frac{1}{2}$f(1)=$\frac{1}{2}$,$f(1-\frac{1}{3})=1-f(\frac{1}{3})$,∴$f(\frac{2}{3})$=$\frac{1}{2}$.
∴当$\frac{1}{3}≤x≤\frac{2}{3}$时,f(x)=$\frac{1}{2}$.
∵$\frac{1}{3}<\frac{2}{5}<\frac{7}{15}<\frac{2}{3}$,
∴$f(\frac{2}{5})=f(\frac{7}{15})=\frac{1}{2}$,
∴$f(\frac{2}{5})$+$f(\frac{7}{15})$=1.
故答案为:1.
点评 本题考查了利用导数研究函数的单调性及其应用,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:填空题
 在校英语节演讲比赛中,七位评委老师为某班选手打出的分数的茎叶图(如图所示),去掉一个最高分和一个最低分后,所剩数据的方差为$\frac{8}{5}$.
在校英语节演讲比赛中,七位评委老师为某班选手打出的分数的茎叶图(如图所示),去掉一个最高分和一个最低分后,所剩数据的方差为$\frac{8}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
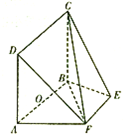 如图,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在平面与平面ABEF互相垂直.
如图,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在平面与平面ABEF互相垂直.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com