
分析 (1)直接把|3$\overrightarrow{a}$-2$\overrightarrow{b}$|=3两边平方,结合$|\overrightarrow{a}{|}^{2}={\overrightarrow{a}}^{2}$求得$\overrightarrow{a}$$•\overrightarrow{b}$的值;
(2)利用平面向量的数量积运算求得$\overrightarrow{m}•\overrightarrow{n}$,再求出$|\overrightarrow{m}|,|\overrightarrow{n}|$,代入数量积公式求得向量$\overrightarrow{m}=2\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{n}=2\overrightarrow{b}-3\overrightarrow{a}$的夹角.
解答 解:(1)由|3$\overrightarrow{a}$-2$\overrightarrow{b}$|=3,得$(3\overrightarrow{a}-2\overrightarrow{b})^{2}=9$,即$9|\overrightarrow{a}{|}^{2}-12\overrightarrow{a}•\overrightarrow{b}+4|\overrightarrow{b}{|}^{2}=9$,
∴$9-12\overrightarrow{a}•\overrightarrow{b}+4=9$,得$\overrightarrow{a}•\overrightarrow{b}=\frac{1}{3}$;
(2)∵$\overrightarrow{a}$、$\overrightarrow{b}$的夹角为60°,
∴$\overrightarrow{m}•\overrightarrow{n}=(2\overrightarrow{a}+\overrightarrow{b})•(2\overrightarrow{b}-\overrightarrow{a})$=$3\overrightarrow{a}•\overrightarrow{b}-2|\overrightarrow{a}{|}^{2}+2|\overrightarrow{b}{|}^{2}=3|\overrightarrow{a}|•|\overrightarrow{b}|cos60°$=$\frac{3}{2}$.
$|\overrightarrow{m}|=\sqrt{(2\overrightarrow{a}+\overrightarrow{b})^{2}}=\sqrt{4|\overrightarrow{a}{|}^{2}+4\overrightarrow{a}•\overrightarrow{b}+|\overrightarrow{b}{|}^{2}}$=$\sqrt{4+4×1×1×\frac{1}{2}+1}=\sqrt{7}$,
$|\overrightarrow{n}|=\sqrt{(2\overrightarrow{b}-3\overrightarrow{a})^{2}}=\sqrt{4|\overrightarrow{b}{|}^{2}-12\overrightarrow{a}•\overrightarrow{b}+9|\overrightarrow{a}{|}^{2}}$=$\sqrt{4-12×1×1×\frac{1}{2}+9}=\sqrt{7}$.
∴$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{\frac{3}{2}}{7}=\frac{3}{14}$.
∴向量$\overrightarrow{m}=2\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{n}=2\overrightarrow{b}-3\overrightarrow{a}$的夹角为arccos$\frac{3}{14}$.
点评 本题考查平面向量的数量积运算,考查了向量模的求法,考查计算能力,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
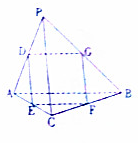 如图,已知三棱锥P-ABC中,点D,E,F,G分别是棱AP,AC,BC,PB上的点,若PA=PB=PC=$\sqrt{2}$,AB=AC=BC=1,且$\frac{AE}{AC}$=$\frac{AD}{AP}$=$\frac{BF}{BC}$=$\frac{BG}{BP}$.
如图,已知三棱锥P-ABC中,点D,E,F,G分别是棱AP,AC,BC,PB上的点,若PA=PB=PC=$\sqrt{2}$,AB=AC=BC=1,且$\frac{AE}{AC}$=$\frac{AD}{AP}$=$\frac{BF}{BC}$=$\frac{BG}{BP}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com